Simple Steps Nodal and Supernode for AC Circuit

The basic of nodal analysis of ac circuit steady-state condition is Kirchhoff’s current law. Nodal and supernode for ac circuit are no different from the dc circuits, so we won’t have big difficulty here.

Nodal and Supernode for AC Circuit

Since KCL is valid for phasors, we can analyze the ac circuit by nodal analysis.

Nodal Analysis of AC Circuit

If you have not learned about its basic principle, make sure to read Nodal Analysis first.

The following nodal analysis ac circuit examples illustrate this.

Find the i_x in the circuit of Figure.(1) using nodal analysis.

Figure 1. Example of nodal ac circuit analysis

Solution :
We first convert the circuit to the frequency domain :

Hence, the frequency domain equivalent circuit is as drawn in Figure.(2).

Figure 2. Frequency domain equivalent of the circuit in Figure.(1)

Applying KCL at node 1,

or

(1.1)

At node 2,

But I_x = V₁/-j2.5. Substituting this gives

By simplifying, we obtain

(1.2)

Equations.(1.1) and (1.2) can be rewritten in matrix form to

We get the determinants as

The current I_x is given by

Transforming this to the time domain,

Read also : balanced wye-delta connection

Supernode Analysis of AC Circuit

Next, we will analyze an ac circuit containing a supernode in the circuit. Like before, we will not cover the basic principle of supernode used in ac circuit.

You need to read Supernode Analysis first in order to understand the following example.

Compute V₁ and V₂ in the circuit of Figure.(3).

Figure 3. Example of supernode ac circuit analysis

Solution :
Nodes 1 and 2 form a supernode as drawn in Figure.(4).

Figure 4. Supernode in the circuit

Applying KCL at the supernode gives

or

(2.1)

But a voltage source is connected between nodes 1 and 2, so that

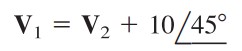(2.2)

Substituting Equations.(2.2) to (2.1) results

From Equation.(2.2),