Brontransformatiestelling – Formule en voorbeelden

Brontransformatiestelling – Uit de vorige berichten hebben we geleerd over reeksen en parallelle verbindingen, samen met Y-delta-transformatie. Deze methoden zullen ons enorm helpen bij het vereenvoudigen van een elektrisch circuit. Een andere methode die we kunnen gebruiken is Brontransformatie.

Een elektrisch circuit is opgebouwd uit zowel actieve als passieve elementen. Zoals je al weet, kunnen de actieve elementen energie produceren, terwijl de passieve elementen alleen energie absorberen of omzetten in een andere vorm van energie. De meest voorkomende actieve elementen die we gebruiken zijn spanningsbron en stroombron. Beide kunnen weer worden onderverdeeld in onafhankelijke en afhankelijke bronnen.

Als we het hebben over een onafhankelijke bron, is de opgeslagen energie (spanning of stroom) een vaste waarde. Aan de andere kant heeft de afhankelijke bron waarde afhankelijk van andere variabelen in het circuit (spanning of stroom op een specifieke plek).

Brontransformatiecircuits

De complexiteit van elektrische circuits kan voor elke toepassing variëren. Naast de basiswet van Ohm en de wetten van Kirchhoff hebben we ook de stellingen voor elektrische circuitanalyse:

• Superpositiestelling.
• Thevenin-stelling.
• Norton-stelling.
• Millman-stelling.

Naast de vier hierboven kunnen we ook Brontransformatie gebruiken.

Brontransformatie impliceert de transformatie van de spanningsbron in de stroombron en omgekeerd. Uiteraard zijn er specifieke procedures die we moeten volgen. De volledige uitleg vindt u hieronder.

Brontransformatie werkt volgens het gelijkwaardigheidsbeginsel. We herinneren ons dat de term equivalent is van een circuit waarbij de v-i-karakteristieken identiek zijn aan het originele circuit.

De basis van deze instrumenten is het concept van gelijkwaardigheid. We herinneren ons dat een equivalent circuit een circuit is waarvan de v-i-karakteristieken identiek zijn aan het originele circuit.

Wat is de brontransformatieregel?

Brontransformatie is het gebruik van de wet van Ohm om een bestaande spanningsbron in serie met een weerstand te vervangen door een stroombron parallel met dezelfde weerstand, of omgekeerd. De getransformeerde bronnen worden als identiek beschouwd en kunnen in een circuit door elkaar worden vervangen.

Brontransformatieformule

We herinneren ons dat analysevergelijkingen voor knooppuntspanning of maasstroom worden geschreven met een eenvoudige inspectie van het circuit wanneer de bronnen een onafhankelijke spanningsbron of een onafhankelijke stroombron zijn.

Het is erg handig om vervanging te kunnen uitvoeren tussen een spanningsbron die in serie is geschakeld met een weerstand en een stroombron die parallel is geschakeld met een weerstand. Het voorbeeld van dit idee is te zien in figuur (1). Elke vervanging staat bekend als een brontransformatie.

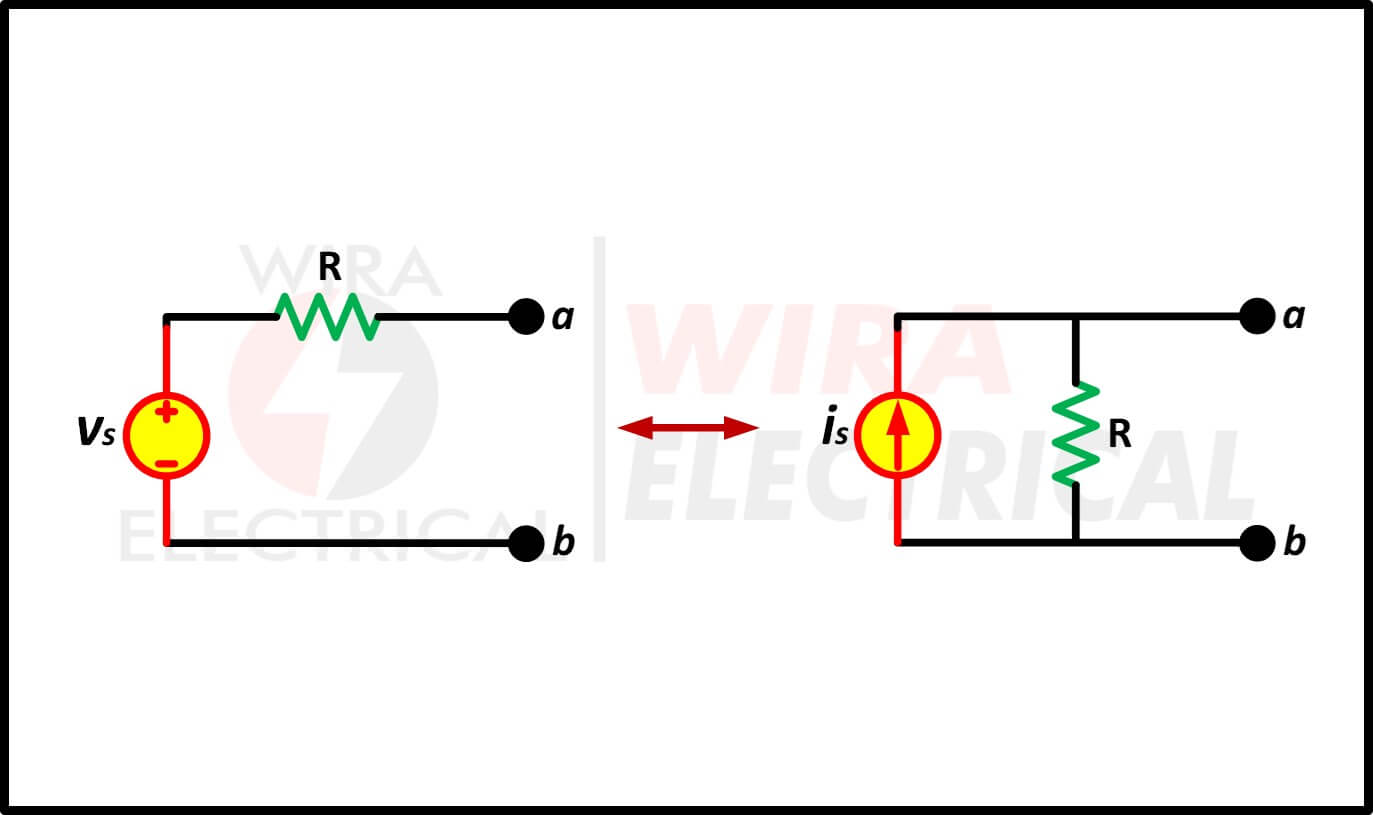
Figuur 1. Brontransformatie

Een brontransformatie is het proces waarbij een spanningsbron in serie met een weerstand R wordt vervangen door een stroombron parallel aan een weerstand R, of omgekeerd.

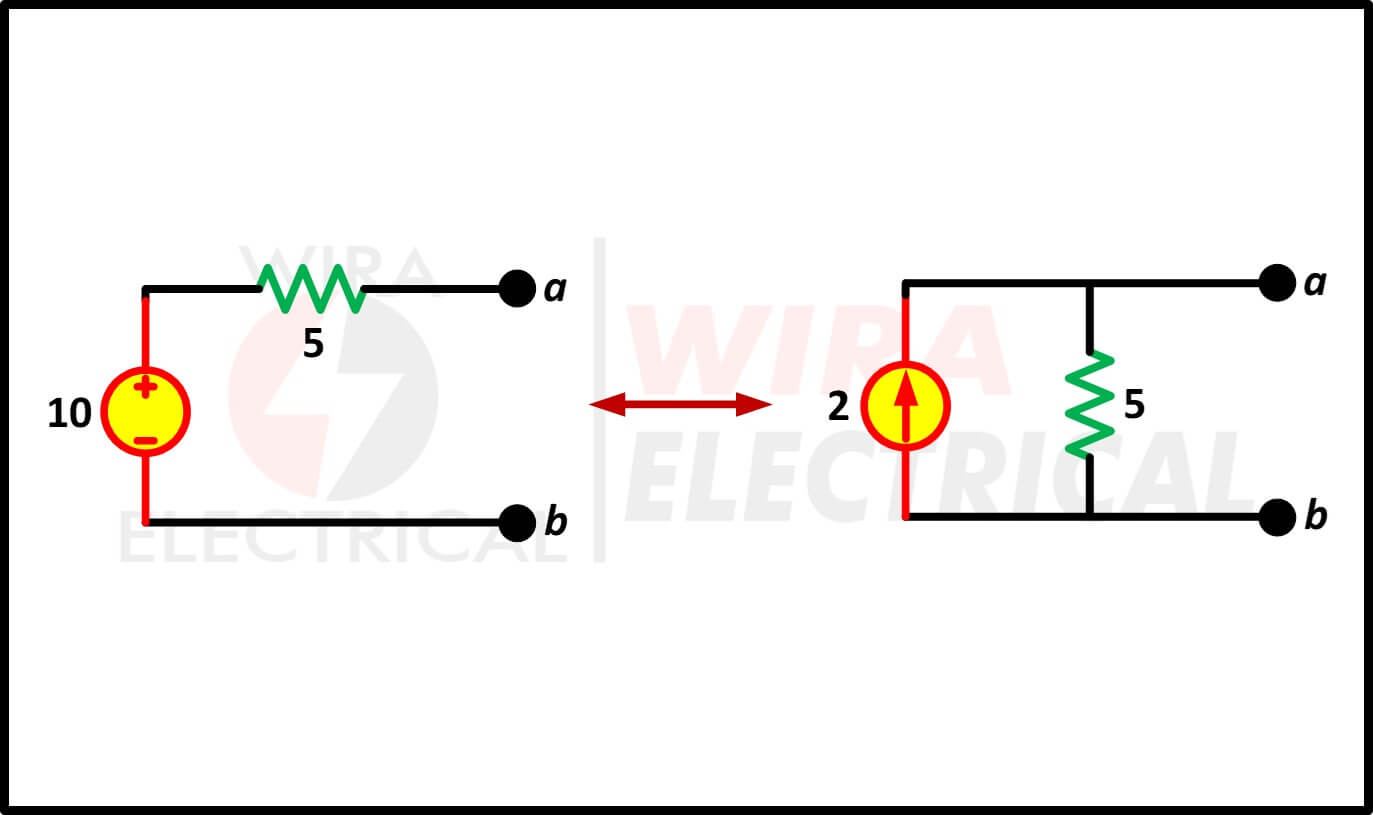
Op het eerste gezicht lijkt het erop dat twee circuits in figuur (2) verschillend zijn, maar in werkelijkheid zijn ze gelijkwaardig omdat ze dezelfde v-i-karakteristieken hebben op de aansluitingen a-b.

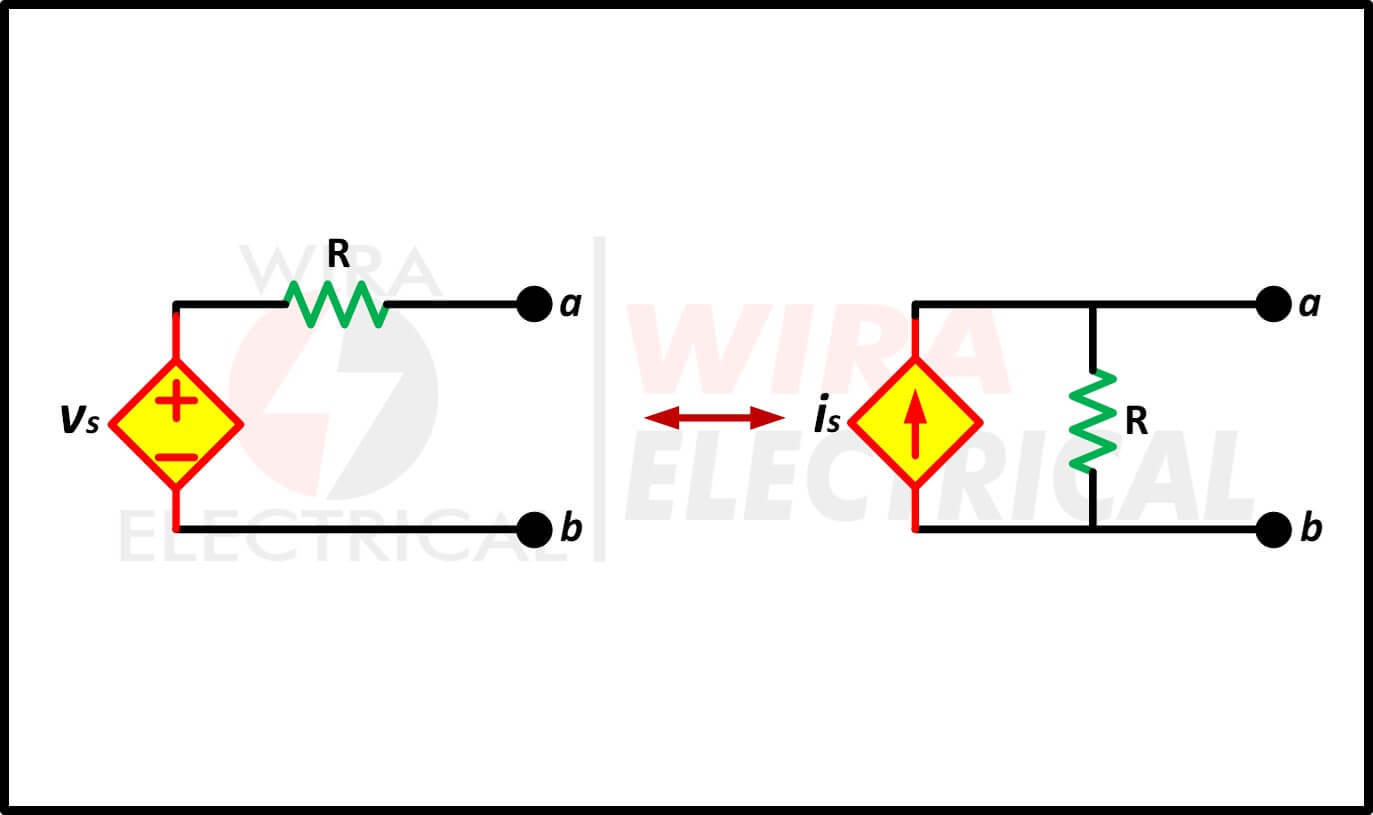
Figuur 2. Brontransformatie

Hoe weten we dat die circuits gelijkwaardig zijn?

Wanneer we hun bronnen uitschakelen, is de equivalente weerstand bij a-b in beide circuits R.

Wanneer we de a-b kortgesloten maken:

• In het circuit aan de bovenzijde stroomt een kortsluitstroom door a-b bij i_sc=v_s/R.
• Het circuit aan de onderkant heeft i_sc=i_s.

Daarom hebben we de v-i-karakteristieken v_s/R=i nodig om twee circuits gelijkwaardig te maken. Hieruit concluderen we dat de brontransformatieformule is geschreven als:

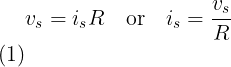
Niet alleen voor onafhankelijke bronnen, ook voor afhankelijke bronnen kunnen we brontransformatie doorvoeren.

We kunnen het voorbeeld in figuur (2) zien, waar we een afhankelijke spanningsbron hebben die in serie is geschakeld met een weerstand. We transformeren dit in een afhankelijke stroombron die parallel is aangesloten op dezelfde weerstand of omgekeerd. We gebruiken ook de bovenstaande vergelijking.(1) om aan de gelijkwaardigheidsregel te voldoen.

Hetzelfde geldt voor de Y-delta-transformatie; deze brontransformatie heeft geen invloed op de rest van het circuit. Dit is een krachtige methode om circuits te manipuleren voor eenvoudigere analyse.

We moeten echter de volgende punten in gedachten houden als we te maken hebben met brontransformatie.

1. Merk op uit figuren (1) of (2) dat de pijl van de stroombron naar de positieve pool van de spanningsbron is gericht.
2. Merk op uit vergelijking (1) dat brontransformatie niet mogelijk is wanneer R = 0, wat het geval is bij een ideale spanningsbron. Voor een praktische, niet-ideale spanningsbron is R ≠ 0. Evenzo kan een ideale stroombron met R = ∞ niet worden vervangen door een eindige spanningsbron.

Nu komt de belangrijke vraag.

Kun je brontransformatie uitvoeren met afhankelijke bronnen?

De brontransformatiestelling is van toepassing op circuits met afhankelijke bronnen.

Brontransformatiestroom naar spanning

Bekijk het onderstaande circuitvoorbeeld om te begrijpen hoe u brontransformatie van stroom naar spanning uitvoert. Natuurlijk heeft het circuit een stroombron en moeten we deze omzetten in een spanningsbron.

We kunnen de stroombron omzetten in een spanningsbron met de onderstaande formule.

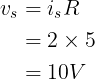
Brontransformatie Spanning naar stroom

Bekijk het onderstaande circuitvoorbeeld om te begrijpen hoe u de brontransformatiespanning naar stroom moet uitvoeren. Natuurlijk heeft het circuit een spanningsbron en moeten we deze omzetten in een stroombron.

We kunnen de stroombron omzetten in een spanningsbron met de onderstaande formule.

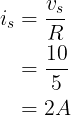
Voorbeelden van brontransformatie

Laten we voor een beter begrip de problemen met brontransformatie bekijken met de onderstaande oplossingen:

1.) Gebruik brontransformatie om v_o te vinden in het circuit van figuur (3).

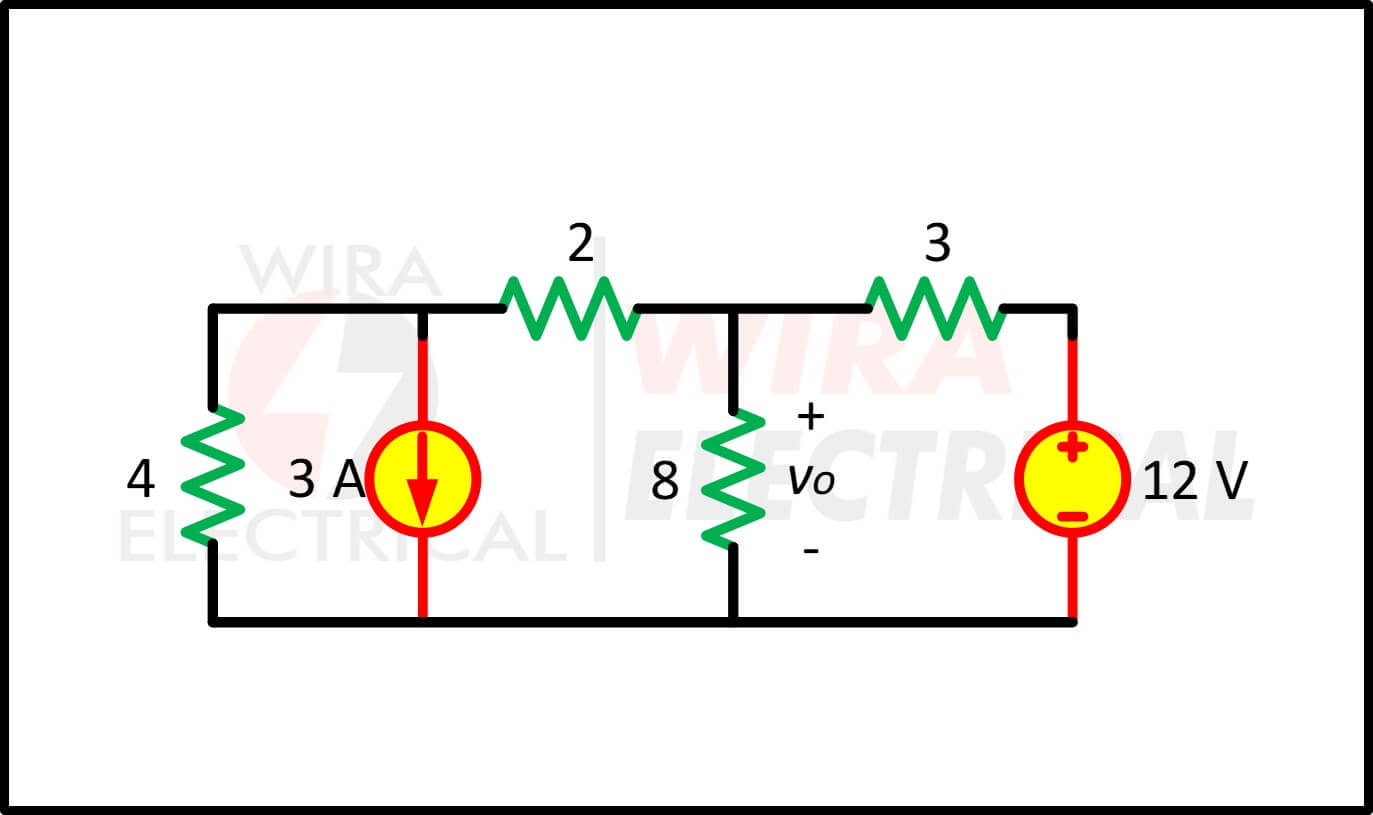
figuur 3

Oplossing :

We transformeren eerst de stroom- en spanningsbronnen om het circuit in figuur (4a) te verkrijgen. De stroombron wordt vervangen door een spanningsbron door:

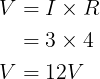
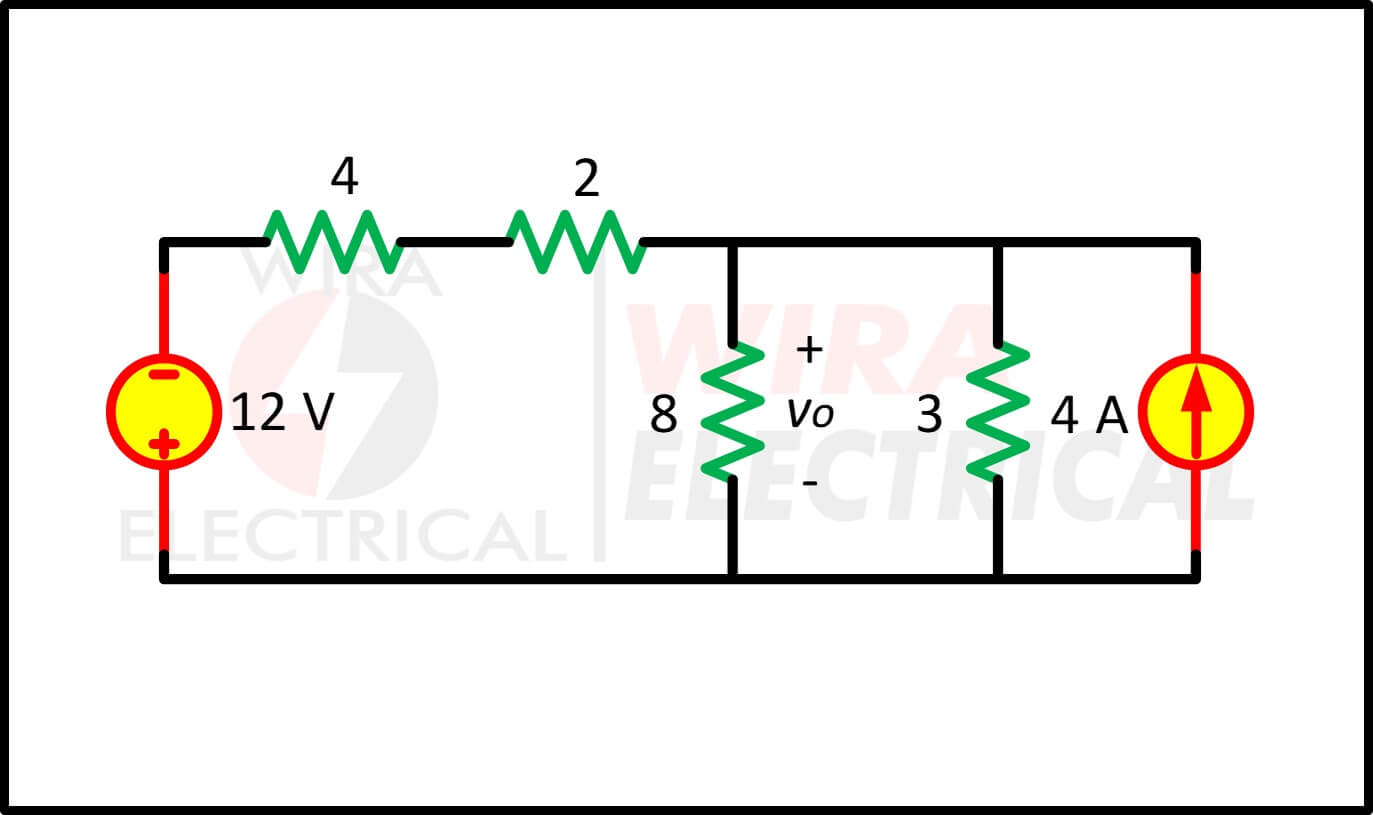
Figuur 4.(a)

Door de weerstanden van 4 Ω en 2 Ω in serie te combineren, ontstaat een weerstand van 6 Ω. Het transformeren van de 12 V-spanningsbron geeft ons figuur (4b). De huidige bronwaarde wordt geschreven door:

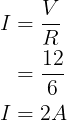
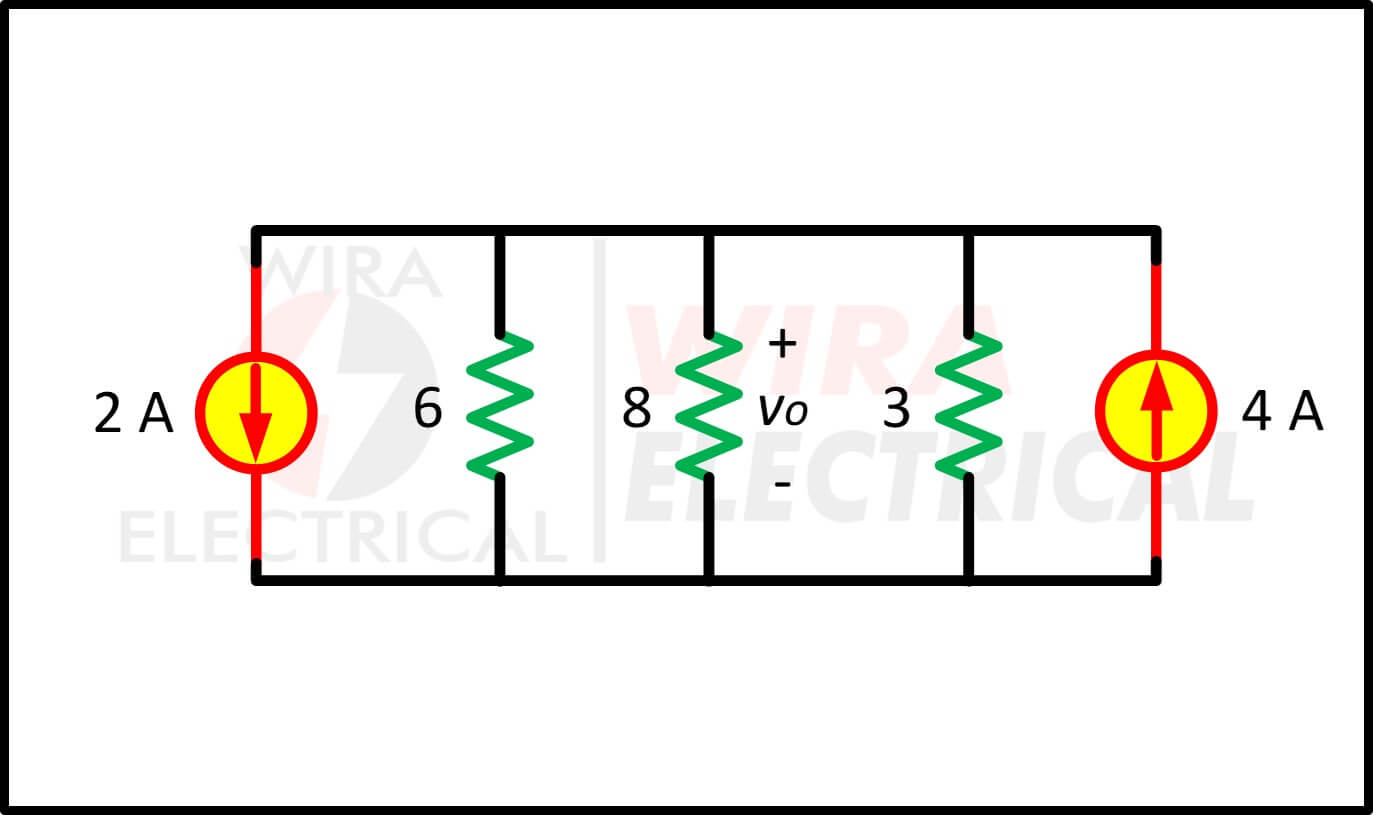
Figuur 4.(b)

We combineren nu de weerstanden van 3 Ω en 6 Ω parallel om 2 Ω te krijgen.

We combineren ook de 2 A- en 4 A-stroombronnen om 2 A-bronnen te krijgen. Door herhaaldelijk brontransformaties toe te passen, verkrijgen we dus het circuit in figuur (4c).

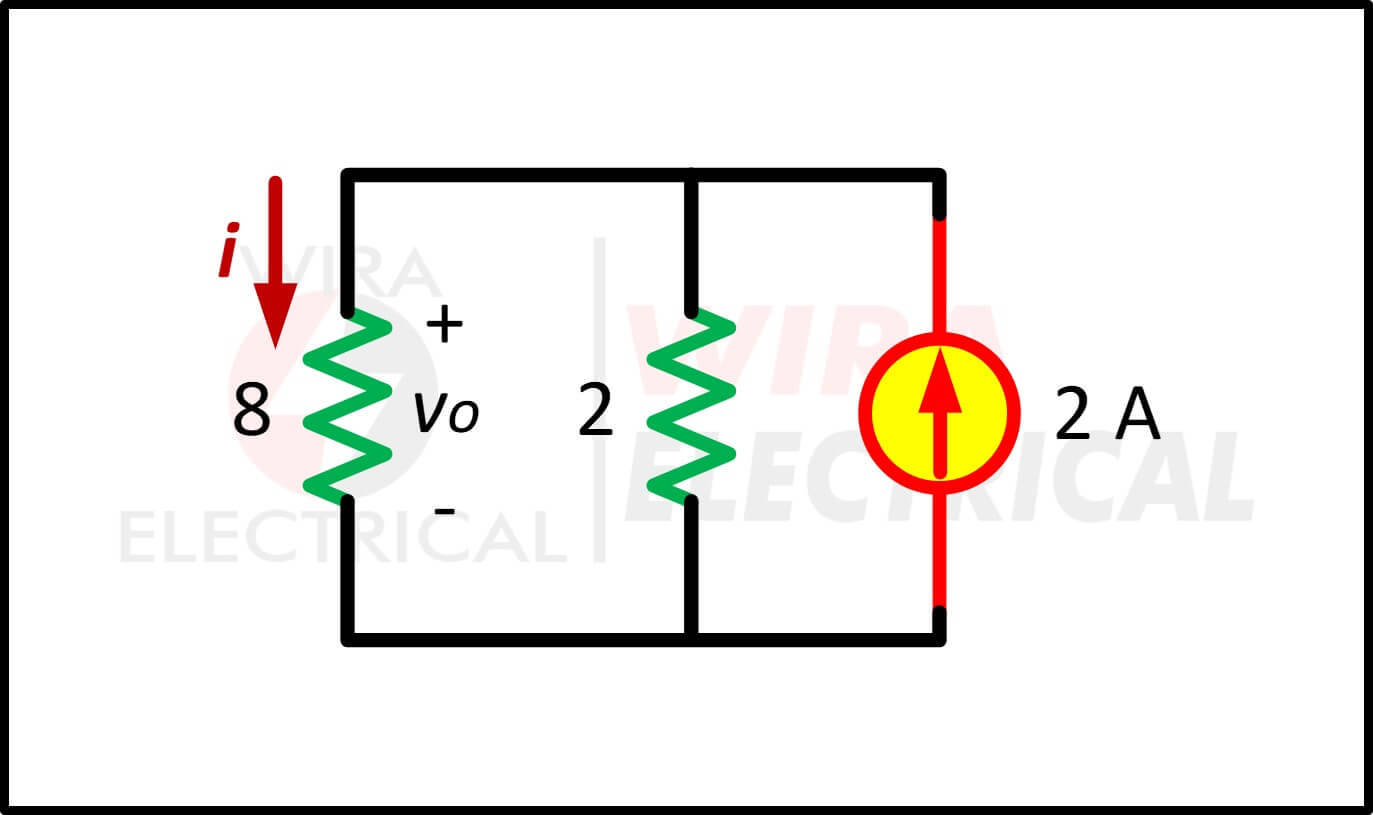
Figuur 4.(c)

We gebruiken de huidige deling in figuur (4c) om te verkrijgen

En

Als alternatief, aangezien de weerstanden van 8 Ω en 2 Ω in figuur (4c) parallel staan, hebben ze dezelfde spanning v_o erover. Vandaar,

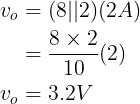
2.) Zoek v_x in figuur (5) met behulp van brontransformatie.

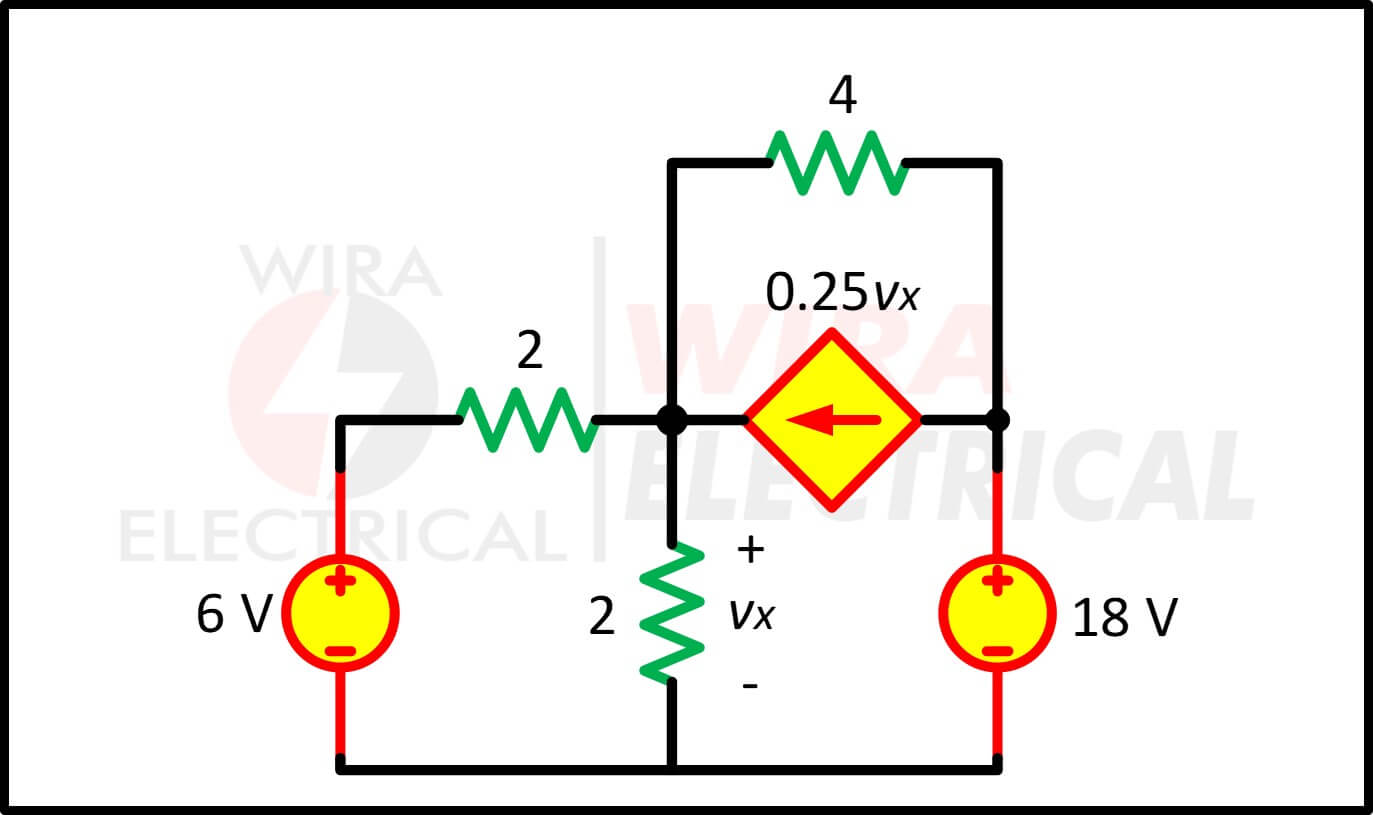
Figuur 5

Hier leren we over brontransformatie met afhankelijke bronnen.

Het circuit in figuur (5) omvat een spanningsgestuurde afhankelijke stroombron. We transformeren deze afhankelijke stroombron en de onafhankelijke spanningsbron van 6 V, zoals weergegeven in figuur (6a). De 18 V-spanningsbron wordt niet getransformeerd omdat deze niet in serie is geschakeld met een weerstand.

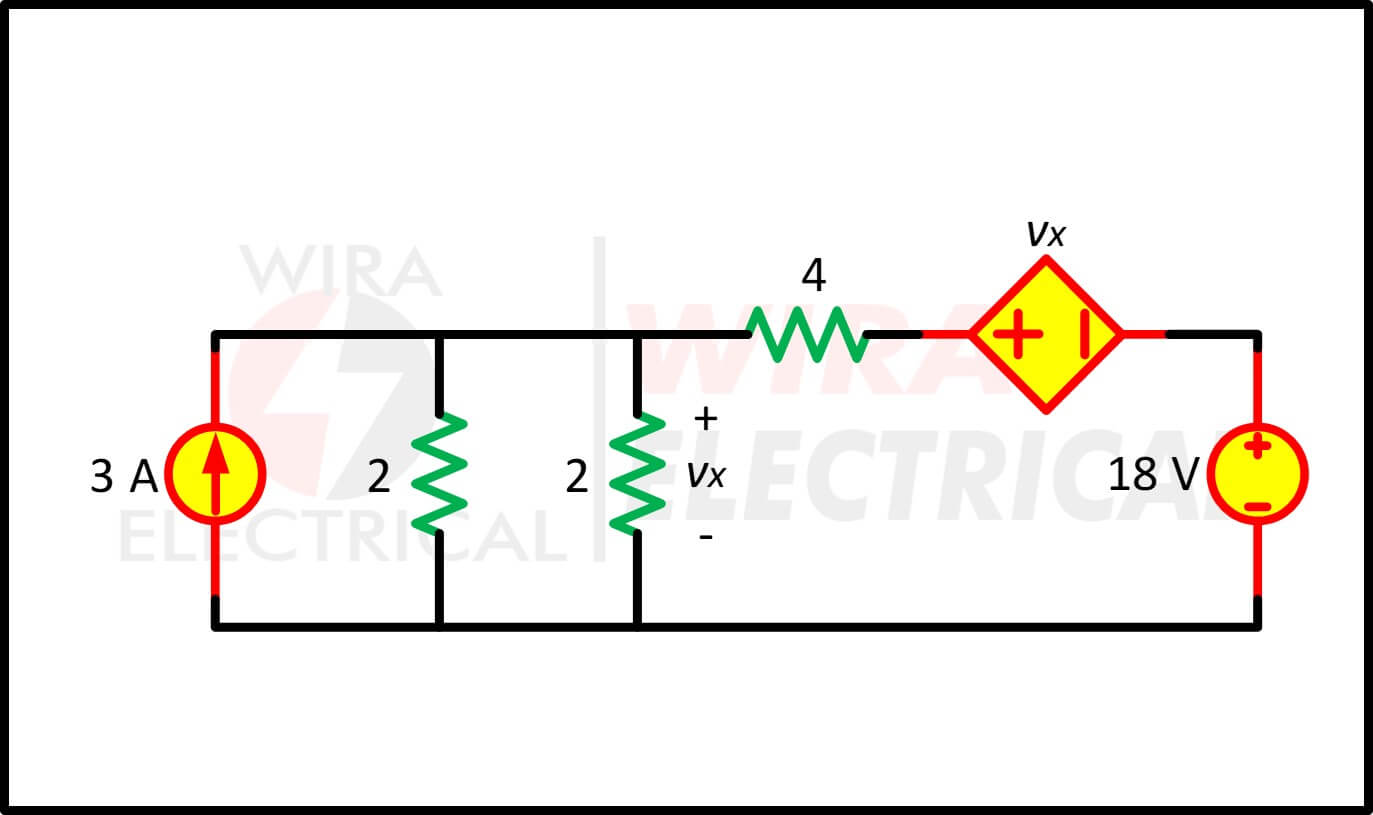
Figuur 6.(a)

De twee parallel geschakelde 2 Ω vormen samen een weerstand van 1 Ω, die parallel staat aan de stroombron van 3 A.

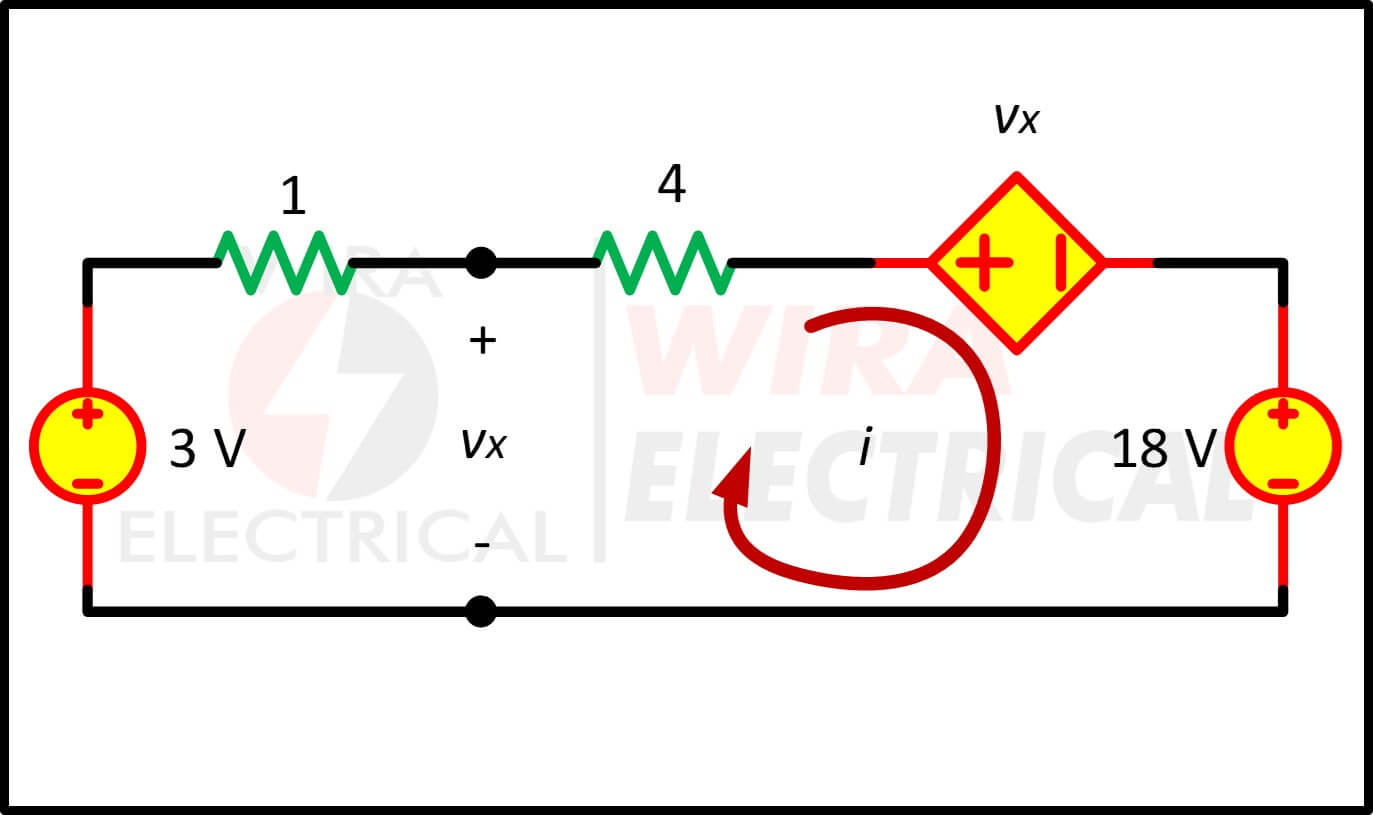
Figuur 6.(b)

De stroombron wordt getransformeerd naar een spanningsbron zoals weergegeven in figuur (6b). Merk op dat de terminals voor vx intact zijn. Het toepassen van KVL rond de lus in figuur (6b) geeft

Het toepassen van KVL op de lus die alleen de 3 V-spanningsbron, de 1 Ω-weerstand en v_x-opbrengsten bevat

Als we dit in (2.1) invullen, krijgen we

Als alternatief kunnen we KVL toepassen op de lus met v_x, de weerstand van 4 Ω, de spanningsgestuurde afhankelijke spanningsbron en de 18 V-spanningsbron in figuur (6b). We krijgen

Dus,