Laplace Transform Integrodifferential Equation is the method of using both integral and derivative for unknown equations using Laplace transform.
Laplace Transform Integrodifferential Equation
The Laplace transform is useful in solving linear integrodifferential equations. Using the differentiation and integration properties of Laplace transforms, each term in the integrodifferential equation is transformed.
Initial conditions are automatically taken into account. We solve the resulting algebraic equation in the s-domain. We then convert the solution back to the time domain by using the inverse transform. The following examples illustrate the process.
Read also : dependent vs independent sources
Laplace Transform Integrodifferential Equation Examples
1. Use the Laplace transform to solve the differential equation
subject to v(0) = 1, v(0) = −2.
Solution:
We take the Laplace transform of each term in the given differential equation and obtain
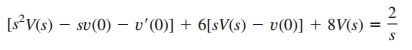
Substituting v(0) = 1, v(0) = −2,
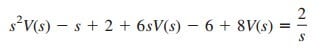
or
Hence,
where
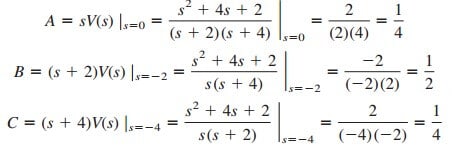
Hence,
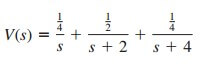
By the inverse Laplace transform,
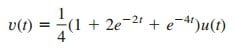
2. Solve for the response y(t) in the following integrodifferential equation.
Solution:
Taking the Laplace transform of each term, we get
Substituting y(0) = 2 and multiplying through by s,
or
where
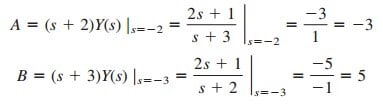
Thus
Its Laplace inverse transform is
