The digital to analog converter (DAC) transforms digital signals into analog form. Of course there is a digital to analog converter formula for us to use.
After learning what is operational amplifier, we will also learn:
- Ideal op amp
- Summing amplifier
- Difference amplifier
- Cascaded op amp circuits
- Digital to analog converter
Digital to Analog Converter
A typical example of a four-bit DAC is illustrated in Figure.(1a). The four-bit DAC can be realized in many ways. A simple realization is the binary weighted ladder, shown in Figure.(1b).
The bits are weights according to the magnitude of their place value, by descending value of Rf/Rn so that each lesser bit has half the weight of the next higher. This is obviously an inverting summing amplifier. The output is related to the inputs as shown in Equation.(3) in the Summing Amplifier.
Thus,
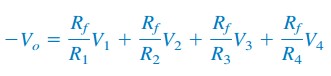
Input V1 is called the most significant bit (MSB), while input V4 is the least significant bit (LSB). Each of the four binary inputs V1, . . . , V4 can assume only two voltage levels: 0 or 1 V. By using the proper input and feedback resistor values, the DAC provides a single output that is proportional to the inputs.
Read also : three-phase power measurement
Digital to Analog Converter Formula Example
In the op amp circuit of Figure.(1b), let:
Rf = 10 k Ω, R1 = 10 k Ω, R2 = 20 kΩ, R3 = 40 kΩ, and R4 = 80 kΩ.
Obtain the analog output for binary inputs:
[0000], [0001], [0010], . . . , [1111].
Solution:
Substituting the given values of the input and feedback resistors in Equation.(1) gives

Using this equation,
a digital input [ V1V2V3V4] = [0000] produces an analog output of –Vo = 0 V;
[V1V2V3V4] = [0001] gives –Vo = 0.125 V.
Similarly,

Table.(1) summarizes the result of the digital-to-analog conversion. Note that we have assumed that each bit has a value of 0.125 V. Thus,in
this system, we cannot represent a voltage between 1.000 and 1.125, for
example. This lack of resolution is a major limitation of digital-to-analog conversions.

For greater accuracy, a word representation with a greater number of bits is required. Even then a digital representation of an analog voltage is never exact. In spite of this inexact representation, digital representation has been used to accomplish remarkable things such as audio CDs and digital photography.