Supernode-analyse eenvoudig op te lossen - Wira Elektrotechniek Portal

Als de vergelijkingen niet correct worden weergegeven, gebruik dan de bureaubladweergave

Contents show

Supernode-analyse of supernodale-analyse wordt nog steeds beschouwd als knooppunt- of knooppuntanalyse, maar met een speciaal geval waarin een spanningsbron in een elektrisch circuit bestaat. Als we goed observeren of de knoopanalyse grondig lezen, vermijden we het analyseren van een elektrisch circuit met een spanningsbron met behulp van knoopanalyse.

Weet u waarom?

De eenvoudige knoopanalyse kan een elektrisch circuit met een spanningsbron niet oplossen. We moeten het circuit een beetje aanpassen voordat we knoopanalyse toepassen. Het modificerende circuit en het oplossen ervan met de knoopanalyse wordt supernodale of supernode-analyse genoemd.

Nadat we deze analysemethode hebben geleerd, hoeven we niet meer te vermijden om knoopanalyse te gebruiken voor een circuit met een spanningsbron.

Lees dit onderwerp grondig door om volledig te begrijpen over supernode-analyse, supernode-voorbeelden en probleemoplossing, en natuurlijk enkele supernode-voorbeelden om ons te helpen onthouden hoe we het moeten gebruiken.

Omdat het supernode-analyse wordt genoemd, denken sommigen van jullie misschien dat deze methode moeilijker is dan nodale analyse. Zelfs als we het circuit moeten aanpassen, is deze supernode-analyse net zo eenvoudig als een knoopanalyse.

Laten we meteen beginnen met de theorie. We zullen ook leren over supernode-analyseproblemen met oplossingen.

Supernode-analysetheorie

Zoals de naam al aangeeft, wordt een supernode nog steeds beschouwd als knooppuntanalyse, omdat de belangrijkste focus nog steeds de knooppunten is. Is nodale analyse gemakkelijker te gebruiken dan supernode-analyse? Ze zullen voor verschillende gevallen worden gebruikt, dus we kunnen niet zeggen welke gemakkelijker is. Het is gewoon een knoopanalyse met een supernode.

Nodale analyse lijkt eenvoudiger, maar is beperkt tot de stroombron in het circuit, zonder een enkele spanningsbron. Daarom kunnen we hier niet op vertrouwen om een schakeling met een spanningsbron op te lossen. Dit is waar supernode-analyse van pas komt.

Laten we het onderstaande circuit bekijken en het verschil zien met het vorige circuit dat we hebben in knoopanalyse.

Heb je het verschil gezien?

Het bovenstaande circuit heeft alleen spanningsbronnen zonder een enkele stroombron. Wat kunnen we uit het circuit halen? Wat is een supernode in een circuit?

Het bovenstaande circuit heeft twee gevallen:

GEVAL 1 – Observeer de 10V-bron op de meest linkse tak die is verbonden met niet-referentieknooppunt v₁ en referentieknooppunt (aardknooppunt).

Dit geval is heel eenvoudig, we hoeven geen enkele wijziging of geavanceerde analyse uit te voeren. Aangezien er alleen een spanningsbron is aangesloten tussen deze twee knooppunten, heeft de knooppuntspanning v₁ dezelfde waarde als de spanningsbron.

$\begin{align*}v_{1}=10V\end{align*}$

Een enkele spanningsbron in een tak maakt het echt eenvoudig door deze kennis van spanning.

Het tweede geval zal extra inspanning vergen om op te lossen omdat er een spanningsbron is tussen twee niet-referentieknooppunten v₂ en v₃. Deze twee knooppunten vormen wat we gegeneraliseerde knooppunten of superknooppunten noemden. We kunnen nog steeds KCL en KVL gebruiken om knooppuntspanningen te berekenen.

Houd bij het definiëren van supernode rekening met het volgende:

Een supernode wordt gevormd wanneer een spanningsbron is aangesloten tussen twee niet-referentieknooppunten en alle parallel daarmee verbonden elementen.

Zoals we hebben geleerd over knoopanalyse, hoeven we alleen KCL te gebruiken om de stroom te vinden die in elke tak of elk element vloeit.

Maar voor een supernode is het onmogelijk om te berekenen hoeveel stroom er door een spanningsbron vloeit. Wat kunnen we dan doen? We kunnen elke methode gebruiken om dit te berekenen, maar zorg ervoor dat u voldoet aan de KCL op de supernode, net als bij elk ander knooppunt.

Eerst schrijven we de KCL-vergelijking voor het bovenstaande circuit,

$\begin{align*}i_{1}+i_{4}&=i_{2}+i_{3}\\\frac{v_{1}-v_{2}}{2}+\frac{v_{1}-v_{3}}{4}&=\frac{v_{2}-0}{8}+\frac{v_{3}-0}{6}\end{align*}$

Dan gebruiken we de KVL voor de supernode. Maar daarvoor moeten we het circuit opnieuw tekenen zoals hieronder wordt weergegeven.

De lus met de klok mee geeft:

$\begin{align*}-v_{2}+5+v_{3}&=0\\v_{2}-v_{3}&=5\end{align*}$

Nadat we de vergelijkingen hebben verkregen, zal het berekenen van de knooppuntspanningen nu eenvoudiger zijn. Nadat we tot nu toe hebben geleerd, moeten we de eigenschappen van de onderstaande supernode-analyse onthouden:

De spanningsbron in de supernode levert de ontbrekende vergelijking om alle knooppuntspanningen op te lossen.
Een supernode heeft geen eigen spanning.
Een supernode vereist de toepassing van zowel KCL als KVL.

Procedure voor supernode-analyse

De procedure voor supernode-analyse zal niet anders zijn met de procedure van knoopanalyse die we eerder hebben geleerd, zoals:

Identificeer alle knooppunten in het circuit, inclusief de supernode.
Stel een knooppunt in als referentieknooppunt. Het fungeert meestal als een grond, dus voeg er gewoon een grondsymbool aan toe.
Wijs knooppuntspanning toe aan andere knooppunten (v₁, v₂, v₃, enz.).
Verwijder eerst de spanningsbron van het circuit.
Schrijf de KCL-supernodevergelijkingen (stromen die een supernode binnenkomen zijn gelijk aan de stromen die de supernode verlaten).
Gebruik de KVL-vergelijking voor de lus waar een spanningsbron bestaat als u de relatie moet vinden van twee knooppunten waar een spanningsbron bestaat. (Om de ontbrekende vergelijking te voltooien).
Schrijf alle KCL-vergelijkingen die je kunt vinden (maak de som van de uitgaande stroom van een tak gelijk aan nul).
Gebruik substitutie, eliminatie, de regel van Cramer, enz.

Om het gemakkelijker te maken, springt u gewoon naar de onderstaande voorbeelden. Veel plezier!

Voorbeelden van supernode-analyse

Nu zullen we proberen de problemen met de supernodes met onderstaande antwoorden beter te begrijpen.

1. Bekijk het onderstaande circuit en zoek de knooppuntspanningen.

Oplossing:

Net zoals we eerder hebben gelezen, wordt een supernode gevormd wanneer een spanningsbron is aangesloten tussen twee niet-referentieknooppunten en alle elementen die er parallel mee zijn verbonden. In ons geval bestaat de supernode uit een 2V-bron, knooppunten 1 en 2 en de 10Ω-weerstand. We verwijderen die om het onderstaande circuit opnieuw te tekenen:

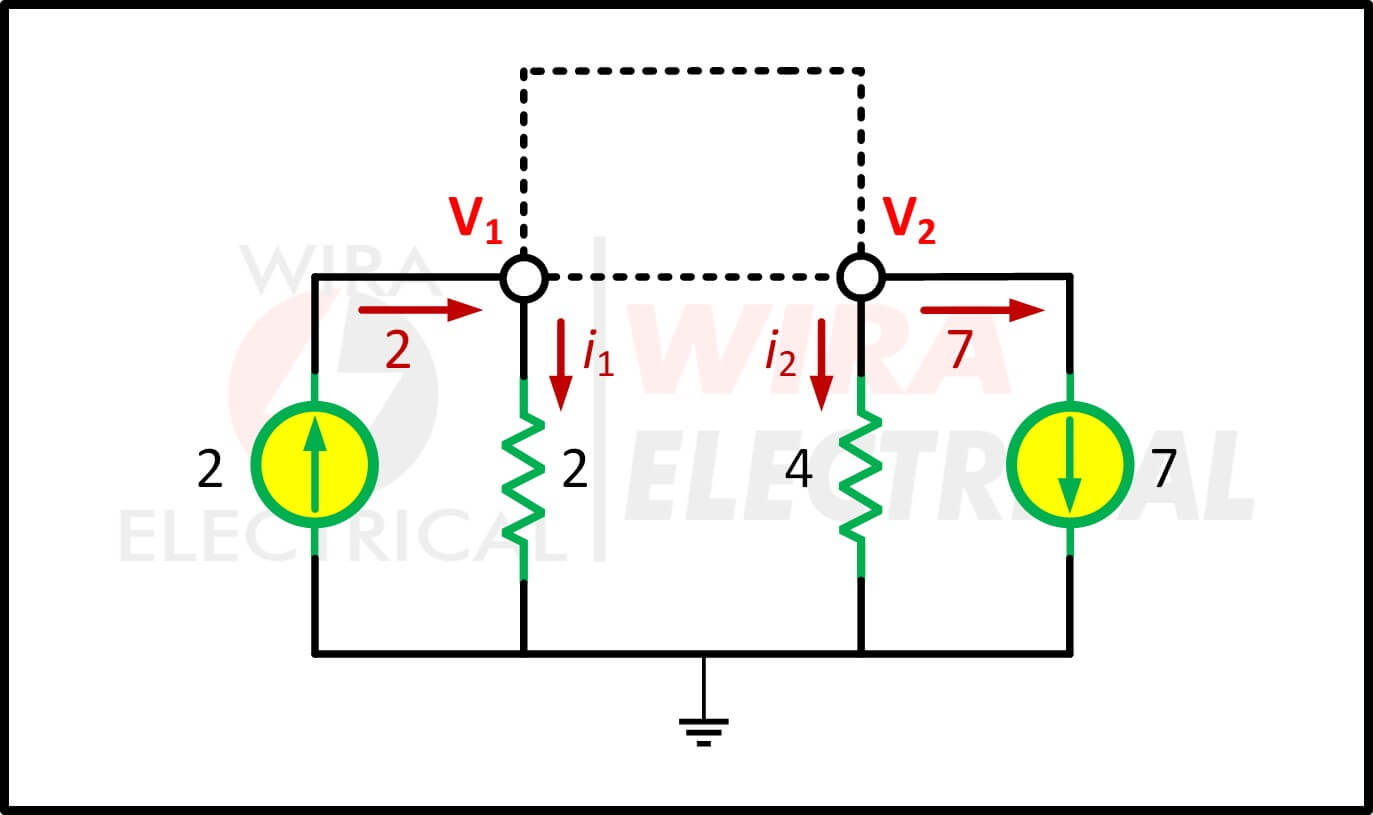
We gebruiken de KCL voor de bovenstaande supernode en we krijgen

$\begin{align*}2=i_{1}+i_{2}+7\end{align*}$

Het schrijven van de KCL-vergelijking voor i₁ en i₂ met behulp van knooppuntspanningsvariabelen geeft,

(1.1) $\begin{align*}2&=\frac{v_{1}-0}{2}+\frac{v_{2}-0}{4}+7\\8&=2v_{1}+v_{2}+28\\v_{2}&=-20-v_{1}\end{align*}$

We missen nog steeds de relatie tussen v₁ en v₂, we zullen KVL gebruiken voor het onderstaande circuit.

Van de lus met de klok mee krijgen we

(1.2) $\begin{align*}-v_{1}-2+v_{2}&=0\\v_{2}&=v_{1}+2\end{align*}$

Uit vergelijkingen (1.1) en (1.2) krijgen we

$\begin{align*}v_{2}=v_{1}+2&=-20-2v_{1}\\3v_{1}=-22 \quad&\rightarrow\quad v_{1}=-7.333V\end{align*}$

we krijgen

$\begin{align*}v_{2}=v_{1}+2=-5.333V\end{align*}$

Merk op dat het bestaan van een 10Ω-weerstand niets zal doen, omdat deze alleen via de supernode is aangesloten.

2. Zoek de knooppuntspanningen in het onderstaande circuit. Dit circuit zal meer tijd in beslag nemen omdat we knoopanalyse zullen doen met 2 supernodes.

Oplossing:

Er zijn twee supernodes in het circuit, het zijn knooppunten 1 en 2, ook knooppunten 3 en 4. Bekijk het bovenstaande circuit en gebruik KCL voor twee supernodes.

Voor supernode 1 en 2,

$\begin{align*}i_{3}+10=i_{1}+i_{2}\end{align*}$

Het gebruik van de termen van de knooppuntspanningen voor de supernode 1-2-vergelijking geeft,

(2.1) $\begin{align*}\frac{v_{3}-v_{2}}{6}+10=\frac{v_{1}-v_{4}}{3}+\frac{v_{1}}{2}\\5v_{1}+v_{2}-v_{3}-2v_{4}=60\end{align*}$

Voor supernode 3-4 hebben we de KCL-vergelijking samen met de knooppuntspanningen,

(2.2) $\begin{align*}i_{1}&=i_{3}+i_{4}+i_{5}\\\frac{v_{1}-v_{4}}{3}&=\frac{v_{3}-v_{2}}{6}+\frac{v_{4}}{1}+\frac{v_{3}}{4}\\4v_{1}+2v_{2}&-5v_{3}-16v_{4}=0\end{align*}$

Vervolgens gebruiken we KVL voor de takken die spanningsbronnen hebben, zoals hieronder weergegeven.

Voor lus 1,

(2.3) $\begin{align*}-v_{1}+20+v_{2}&=0\\v_{1}-v_{2}&=20\end{align*}$

Voor lus 2,

$\begin{align*}-v_{3}+3v_{x}+v_{4}=0\end{align*}$

Vergeet dat niet

$\begin{align*}v_{x}=v_{1}-v_{4}\end{align*}$

dan

(2.4) $\begin{align*}3v_{1}-v_{3}-2v_{4}=0\end{align*}$

Voor lus 3,

$\begin{align*}v_{x}-3v_{x}+6i_{3}-20=0\end{align*}$

We weten dat

$\begin{align*}6i_{3}&=v_{3}-v_{2}\\v_{x}&=v_{1}-v_{4}\end{align*}$

Vandaar,

(2.5) $\begin{align*}-2v_{1}-v_{2}+v_{3}+2v_{4}=20\end{align*}$

Om alle vergelijkingen die we hebben te voltooien, hebben we het resultaat nodig van vier knooppuntspanningen (v₁, v₂, v₃ en v₄). Alle vergelijkingen (2.1) tot (2.5) die we eerder kregen, we hebben er maar vier nodig om de resterende vergelijkingen op te lossen. De vijfde vergelijking is slechts een extra, het kan worden gebruikt om onze berekening dubbel te controleren.

Vervanging van vergelijking (2.3) in respectievelijk (2.1) en (2.2) levert:

(2.6) $\begin{align*}6v_{1}-v_{3}-2v_{4}=80\end{align*}$

(2.7) $\begin{align*}6v_{1}-5v_{3}-16v_{4}=40\end{align*}$

Vergelijkingen (2.4), (2.6) en (2.7) kunnen worden opgelost met behulp van de matrixvorm zoals hieronder weergegeven:

$\begin{align*}\begin{bmatrix}3 & -1 & -2 \\6 & -1 & -2 \\6 & -5 & -16\end{bmatrix}\begin{bmatrix}v_{1}\\v_{3}\\v_{4}\end{bmatrix}=\begin{bmatrix}0\\80\\40\end{bmatrix}\end{align*}$

Dan gebruiken we de regel van Cramer en krijgen

$\begin{align*}\Delta&=\begin{vmatrix}3 & -1 & -2 \\6 & -1 & -2 \\6 & -5 & -16\end{vmatrix}=-18\\\\\Delta_{1}&=\begin{vmatrix}0 & -1 & -2 \\80 & -1 & -2 \\40 & -5 & -16\end{vmatrix}=-480\\\\\Delta_{3}&=\begin{vmatrix}3 & 0 & -2 \\6 & 80 & -2 \\6 & 40 & -16\end{vmatrix}=-3120\\\\\Delta_{4}&=\begin{vmatrix}3 & -1 & 0 \\6 & -1 & 80 \\6 & -5 & 40\end{vmatrix}=840\end{align*}$

Daarom zijn de knooppuntspanningen

$\begin{align*}v_{1}=\frac{\Delta_{1}}{\Delta}=\frac{-480}{-18}=26.67V\\v_{3}=\frac{\Delta_{3}}{\Delta}=\frac{-3120}{-18}=173.33V\\v_{4}=\frac{\Delta_{4}}{\Delta}=\frac{840}{-18}=-46.67V\end{align*}$

$\begin{align*}v_{2}=v_{1}-20=6.667V\end{align*}$

Veel Gestelde Vragen

Wat is een supernode?

Een supernode wordt gevormd wanneer een spanningsbron is aangesloten tussen twee niet-referentieknooppunten en alle parallel daarmee verbonden elementen.

Wat is supernode-analyse?

Supernode-analyse is knoopanalyse wanneer er een spanningsbron bestaat tussen twee niet-referentieknooppunten. Deze analyse zal het circuit manipuleren om aanvullende vergelijkingen te geven om de onbekende variabelen te vinden.

Wanneer supernode gebruiken?

Supernode wordt gebruikt wanneer er een spanningsbron bestaat tussen twee niet-referentieknooppunten en alle parallel daarmee verbonden elementen.