De regel voor stroomverdeling wordt geïmplementeerd in een stroomdeler circuit. Dit circuit gebruikt parallel geschakelde weerstanden in plaats van serie geschakelde weerstanden zoals we hebben geleerd in een spanningsdeler circuit.
Als het spanningsdeler circuit een gelijke stroom door elke weerstand heeft, heeft het stroomdeler circuit een gelijke spanning over elke weerstand.
Stroom Divisie Regel
De regel voor de stroomdeler volgt de wet van Kirchhoff, waarbij de som van alle stromen die een knooppunt binnenkomen gelijk is aan de som van alle stromen die hetzelfde knooppunt verlaten. Elke stroom die een knooppunt binnenkomt en verlaat, wordt bepaald door de weerstand van elke tak die met dat knooppunt is verbonden.
Bekijk het onderstaande DC-circuit.
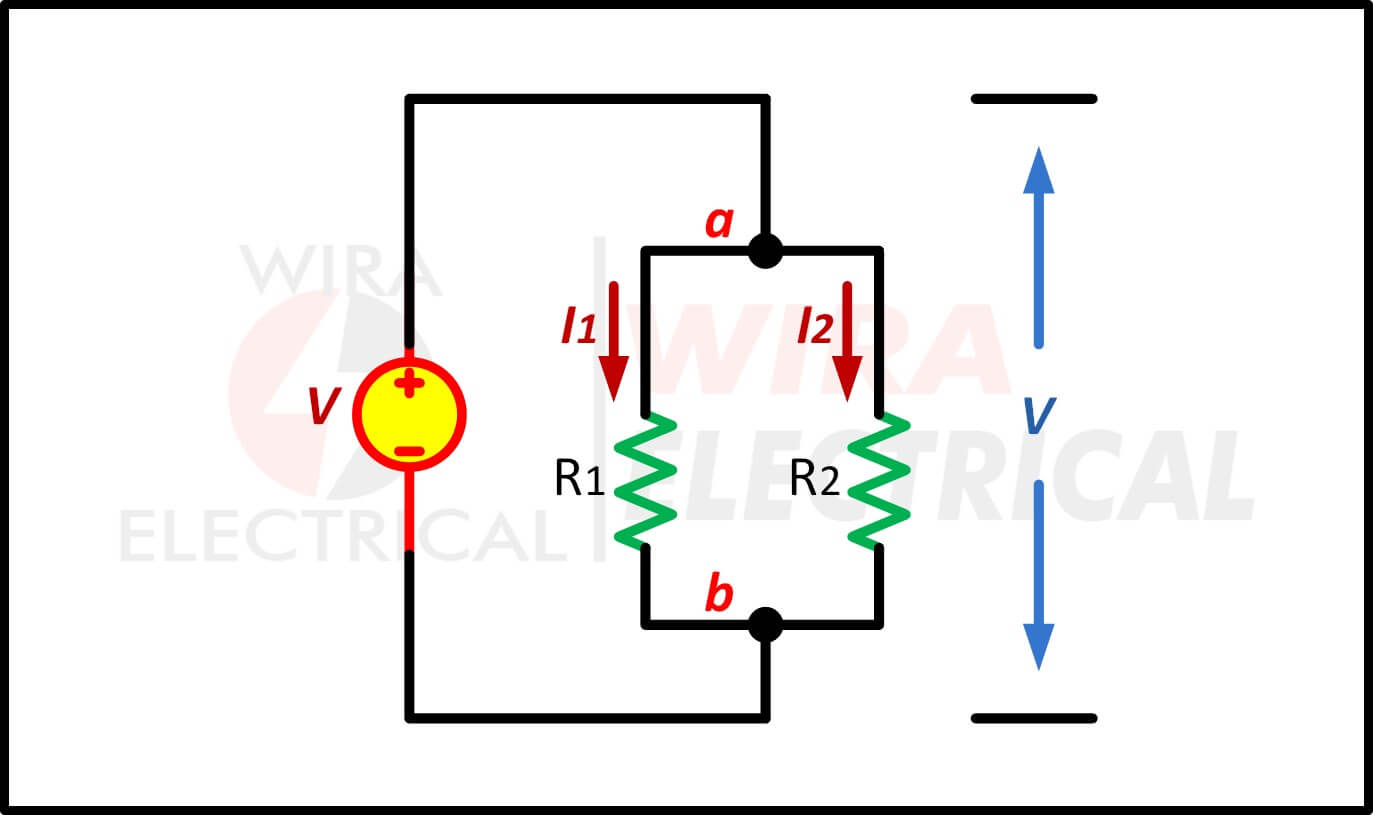
Vanuit de knoop a en b stelt de wet van Kirchhoff dat:
De algebraïsche som van alle stromen die een knooppunt binnenkomen, is gelijk aan de algebraïsche som van alle stromen die een knooppunt verlaten.
Of met andere woorden:
De algebraïsche som van alle stromen die een knooppunt binnenkomen en verlaten, is gelijk aan nul.
De stroom die knooppunt a binnenkomt is gelijk aan de stroom die knooppunt b verlaat. Tussen knooppunt a en b wordt de stroom verdeeld in twee takken, I1 en I2 met hun weerstanden respectievelijk R1 en R2 met V als de spanning over beide weerstanden daalt (R1 en R2).
In een parallelschakeling is de spanningsval over elke weerstand die parallel is geschakeld gelijk aan elkaar (V1 = V2 = V3 …). In een serieschakeling is de stroom die door elke weerstand die in serie is geschakeld gelijk aan elkaar (I1 = I2 = I3 …).
Formule voor de Stroom Deelregel
Gebruik het circuit voorbeeld hierboven om te begrijpen hoe we de Stroom deling formule gebruiken.
Vanuit de wet van Ohm weten we al dat
![]()
Of
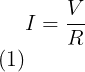
Gebruik dit om de stroom voor elke tak in het circuit te berekenen
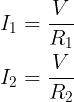
De totale weerstand in dat parallelle circuit is
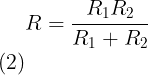
Door vergelijking (2) in (1) te substitueren krijgen we
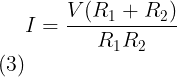
En
![]()
Als we vergelijking (4) in 3 substitueren, krijgen we:
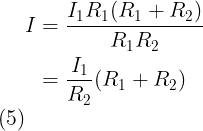
Met behulp van vergelijking (5) maar met I2 en R2, dan
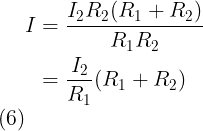
De vergelijkingen (5) en (6) zijn onze Stroom deler formule, waarbij:
De stroom die door parallelle takken loopt, is gelijk aan de verhouding van de tegengestelde weerstand tot de totale weerstand, vermenigvuldigd met de totale stroom.
Het zal heel anders zijn met een circuit dat bestaat uit drie of meer weerstanden die parallel zijn geschakeld.
De equivalente weerstand wordt gedeeld door de weerstand van een tak waar de gewenste stroom doorheen stroomt. Wiskundig gezien is de stroomdeler regel voor 3 weerstanden de totale stroom vermenigvuldigd met de fractie van equivalente weerstand tot de respectieve weerstand van een tak.
Voorbeelden van Stroom Deelregels
Om het makkelijker te begrijpen, zullen we hieronder een paar voorbeelden bekijken.
1. Bekijk het eenvoudige circuit hieronder om op te lossen hoe het stroomdeler circuit met twee weerstanden wordt opgelost.
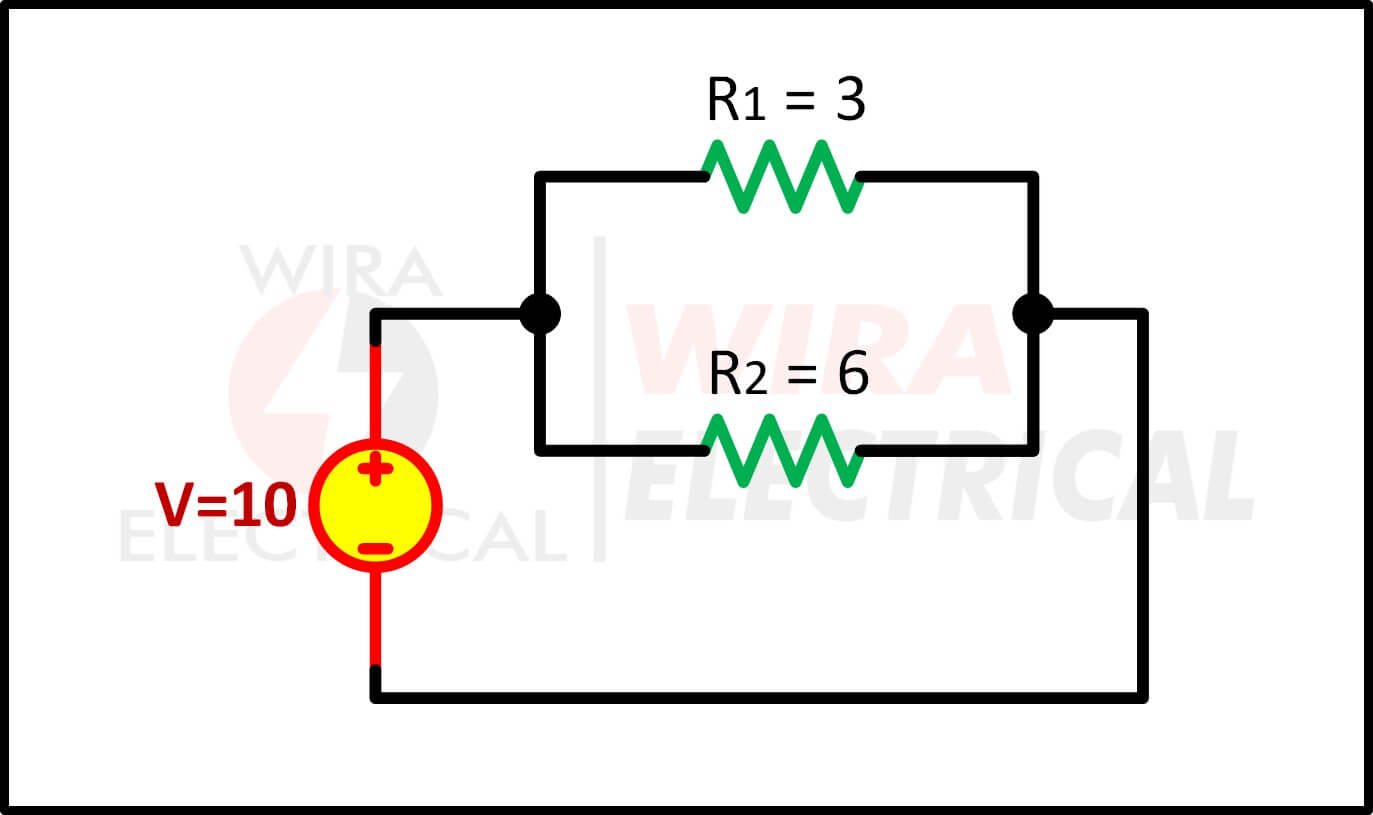
De equivalente weerstand is
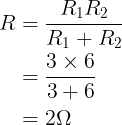
De totale stroom is
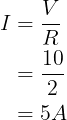
De Stroom I1 is
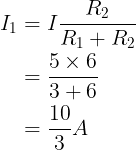
De Stroom I2 is
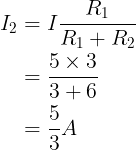
Dit verduidelijkt wat de Stroom wet van Kirchhoff zegt

2. Nu gaan we proberen een stroomdeler regel voor 3 weerstanden op te lossen.
De equivalente weerstand is

De totale stroom is

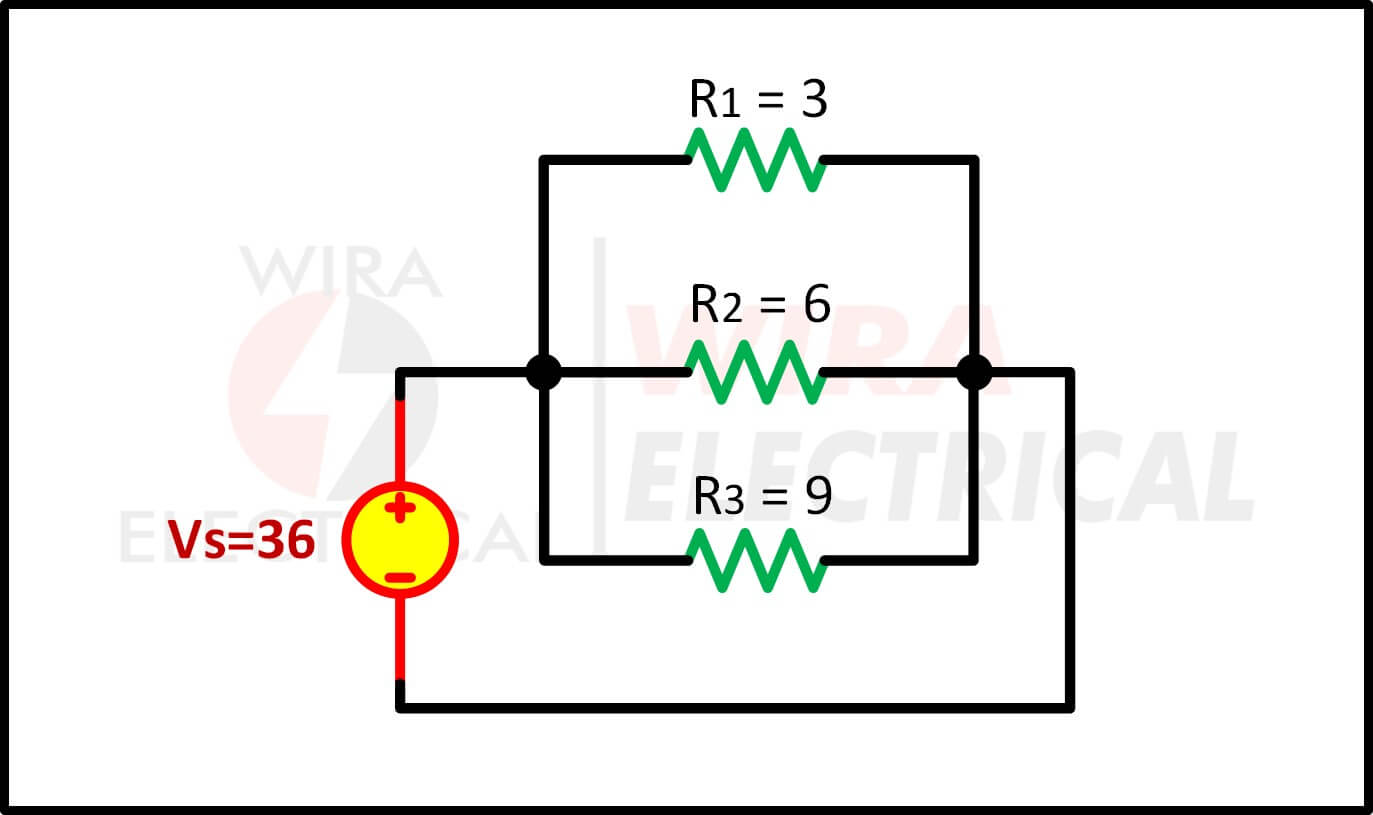
De spanningsval over elke weerstand is
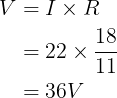
Het equivalente circuit is
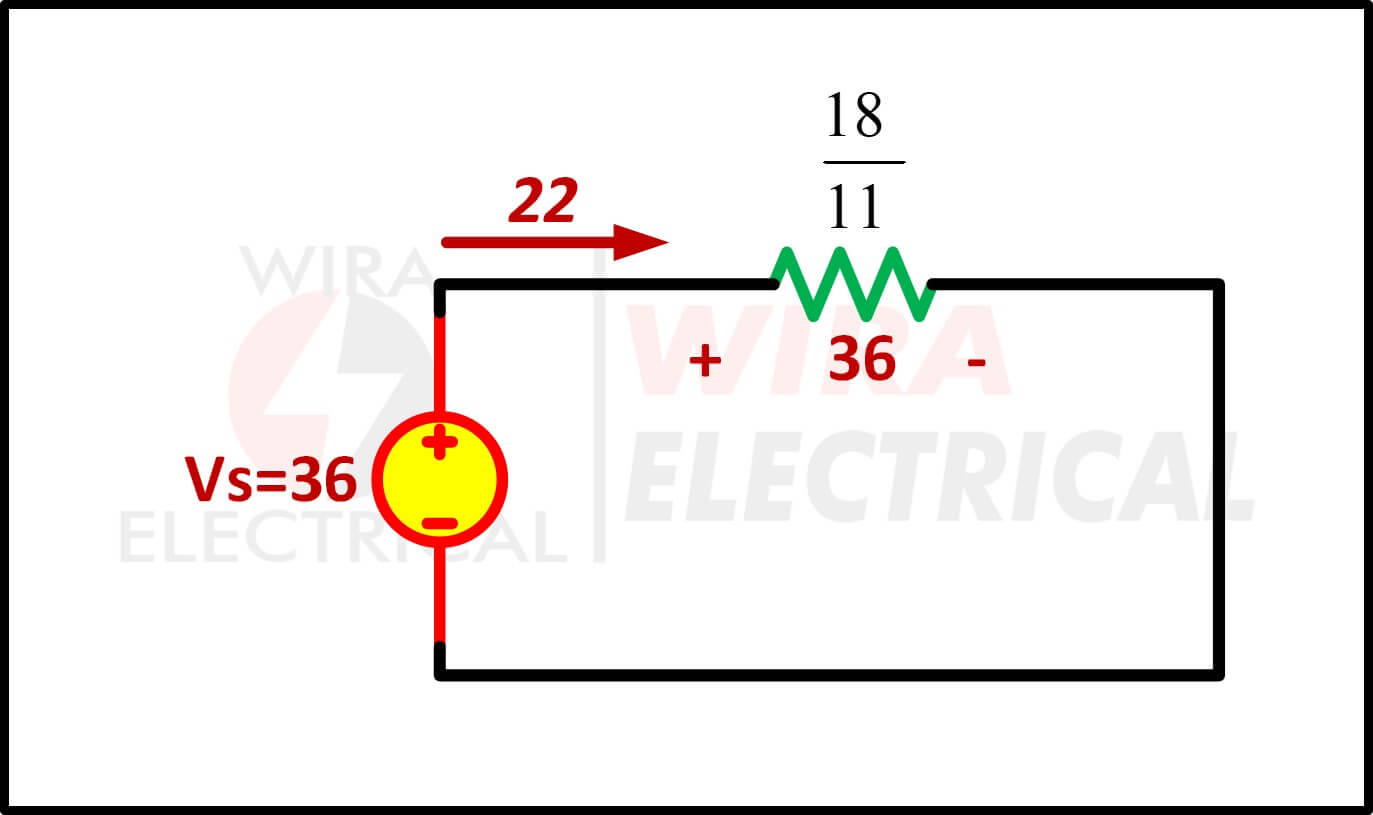
Omdat de parallelschakeling een gelijke spanningsval heeft over elke parallel geschakelde weerstand, dan
![]()
De stroom die door elke tak stroomt, is
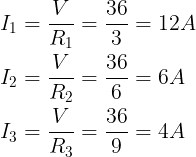
Dit is een veelgebruikte methode om de stroom te vinden die door elke tak stroomt. Maar er is een snelle methode waarbij we direct de equivalente formule gebruiken.
We moeten nog steeds de totale stroom berekenen, uit de bovenstaande vergelijking weten we dat de totale stroom (I) 22 A is.
We gebruiken de bovenstaande vergelijkingen om de I1, I2 en I3 te vinden.
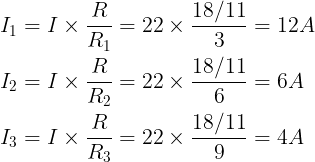
Veelgestelde vragen
Wat is de stroom verdelingsregel?
De stroomverdeling regel stelt dat de stroom die door parallelle takken stroomt gelijk is aan de verhouding van tegengestelde weerstand tot de totale weerstand en vermenigvuldigd met de totale stroom.