Voordat we elektrische circuit analyse leren, moeten we ons vertrouwd maken met het concept van spanningsdeling en stroomdeling in een elektrisch circuit.
Deze keer leren we de spanningsdeling regel en bewaren we de stroomdeler regel voor een andere keer.
Een spanningsdeler is altijd aanwezig in een serieschakeling, terwijl een stroomdeler altijd aanwezig is in een parallelschakeling. Omdat een serieschakeling een constante stroom door alle circuit elementen heeft die in serie zijn geschakeld, wordt de spanning over elk element bepaald door hun impedantiewaarde.
Spanningsverdeling Regel
Om het simpeler te maken, nemen we aan dat we een eenvoudig circuit hebben dat bestaat uit een spanningsbron en meerdere weerstanden. Dit circuit kan eenvoudig worden opgelost met de wet van Ohm.
De spanningsval over elke weerstand is evenredig met de ohmse waarde van de weerstand.
De stroom die door het circuit stroomt, is evenredig met de totale weerstand van alle weerstanden in dat circuit.
Met behulp van de wet van Ohm kunnen we de spanningsval over elke weerstand berekenen als
![]()
De spanning over een weerstand is gelijk aan de stroom die door het circuit stroomt, vermenigvuldigd met de weerstand.
De spanningsverdelingsregel is erg populair omdat het spanningsdeler circuit veel wordt gebruikt voor veel toepassingen. We kunnen een spanningsniveau verdelen in een specifiek percentage van de maximale spanning door alleen de juiste weerstanden te gebruiken.
De spanningsverdeling regel stelt dat:
De totale spanning die over een serieschakeling van meerdere weerstanden wordt geleverd, wordt evenredig over de weerstanden verdeeld.
Dit laat zien dat de grootste spanningsval te vinden is over de weerstand met de hoogste weerstand. Daartegenover staat dat de kleinste spanningsval te vinden is over de weerstand met de laagste weerstand.
Deze spanningsverdeling regel geldt voor zowel AC-circuits als DC-circuits.
Houd er rekening mee dat we impedantie gebruiken in plaats van weerstand bij het werken met een AC-circuit.
Spanningsdeler Regels Formule
Ons doel hier is om de spanning over een specifieke weerstand te kunnen berekenen.
Voordat we begrijpen waarom spanning in serieschakelingen wordt verdeeld, moeten we de relatie tussen de spanning, stroom en weerstand in een serieschakeling begrijpen.
Bekijk hieronder een eenvoudig circuit met n weerstanden.

De totale weerstand in dat circuit is
![]()
De totale stroom die door het circuit stroomt is

Dit is waar we de wet van Ohm gebruiken om de spanning over een specifieke weerstand te berekenen. De spanning over weerstand R1 zal zijn
![]()
De spanning over weerstand R2 zal zijn
![]()
De spanning over de Rn zal zijn
![]()
Als we nu de totale stroomvergelijking vervangen door de spanning over R1, krijgen we:

Als we de totale stroomvergelijking vervangen door de spanning over R2, krijgen we:
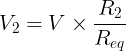
Als we de totale stroomvergelijking vervangen door de spanning over Rn, krijgen we:

Waar:
Vn = spanningsval over de n-de weerstand
Rn = weerstand van de n-de weerstand
De som van de spanningsval over de n-serieweerstanden is gelijk aan de verhouding van de totale stroom gedeeld door de equivalente weerstand van de weerstanden.
We kunnen concluderen dat:
De spanningsval over een n-de weerstand is het product tussen de ingangsspanning en de weerstand van de n-de weerstand, gedeeld door de equivalente serieweerstand.
Dit beantwoordt de vraag waarom spanning in serieschakelingen wordt verdeeld. Dat komt omdat de stroom in een serieschakeling constant is door elke weerstand, terwijl de spanning over elke weerstand afhankelijk is van de weerstand.
Spanningsdeler Regel Formule in serieschakeling
Laten we nog een berekening doen en proberen het volledig te begrijpen.
Bekijk hieronder een eenvoudig circuit bestaande uit een spanningsbron en drie weerstanden in serie geschakeld.
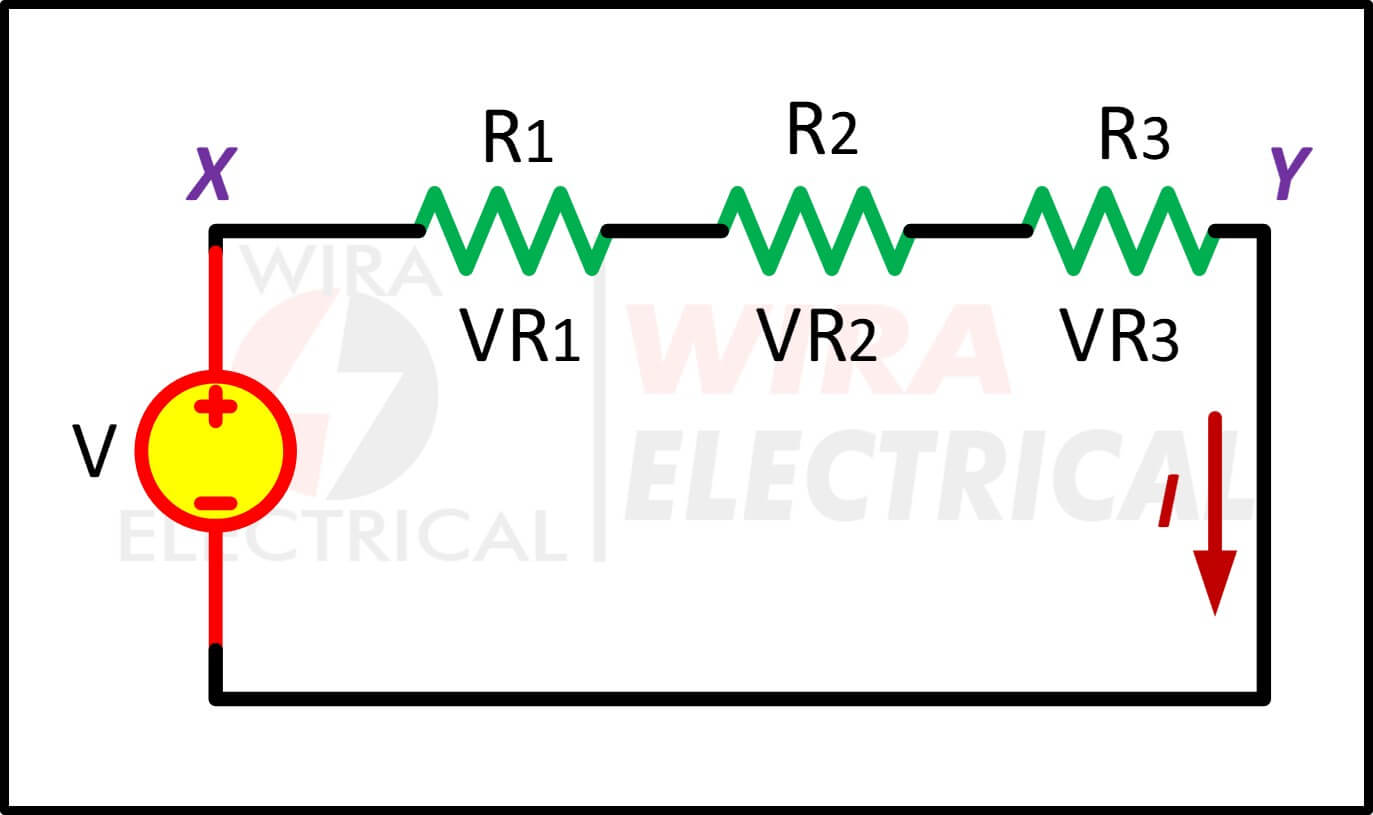
We zoeken nu naar de spanningsval VR1, VR2 en VR3 voor elke weerstand R1, R2 en R3.
Omdat de stroom door elke weerstand gelijk is, zou de spanningsval alleen beïnvloed moeten worden door de weerstandswaarde.
Hoe vind je de individuele spanning in een serieschakeling? Door simpelweg de wet van Ohm te gebruiken voor elke weerstand, wordt deze vraag opgelost. De spanningsval is
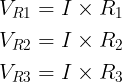
De totale spanning over knooppunt X – Y moet gelijk zijn aan de som van de spanningsdalingen over elke weerstand. Als resultaat kunnen we schrijven:
![]()
Als we elke spanningsval vervangen door de vergelijking hiervoor, krijgen we:
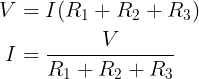
De spanningsverdeling over de individuele weerstand kan hieronder worden berekend

Hoe splitst de spanning zich in serie?
De spanningsverdeling werd geschat met behulp van drie weerstanden in serie. De methode kan worden gebruikt met elk aantal in serie geschakelde weerstanden in een DC-circuit of impedantie in een AC-circuit.
![]()
Houd er rekening mee dat we de volledige weerstand moeten omrekenen naar een equivalente weerstand, ook als we maar één spanningsval willen berekenen.
Spanningsdeler Circuit
Spanningsdeler Circuit is een circuit om het gewenste spanningsniveau te produceren van de spanningsbron, maar de stroom is nog steeds hetzelfde. De algemene configuratie van een spanningsdeler circuit wordt hieronder weergegeven.
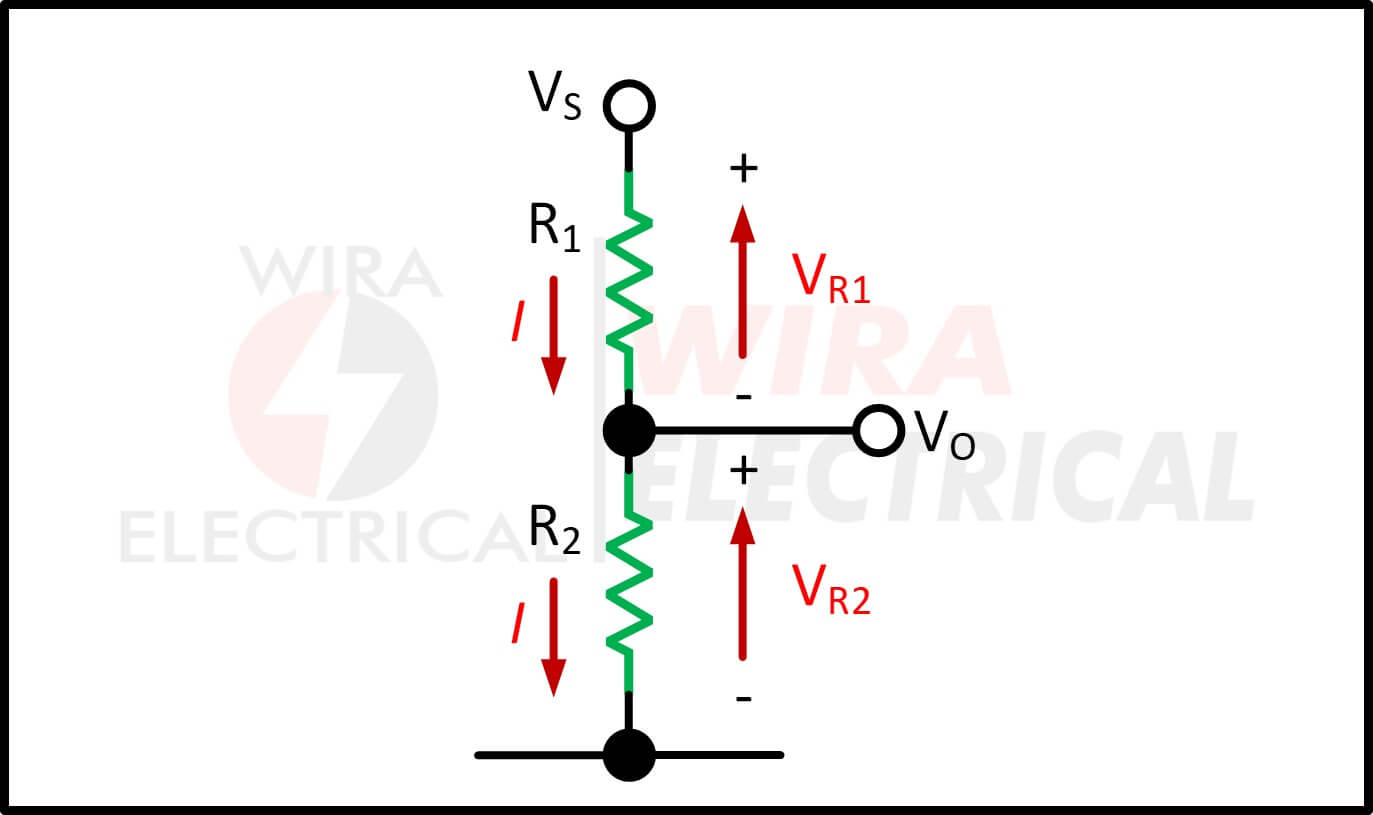
Het enige doel van een spanningsdeler is om de spanningsbron te verdelen in verschillende spanningsniveaus ten opzichte van de grond.
Omdat spanning ook bekend staat als potentiaalverschil, staat een spanningsdeler ook bekend als potentiële deler.
De spanningsbron VS toegepast op de gehele serie weerstanden en we kunnen de spanningswet van Kirchhoff en de wet van Ohm gebruiken om de spanningsval over de gewenste weerstand te berekenen.
De spanningsval over R1 is

De spanningsval over de R2 is

Om de vergelijking te vereenvoudigen, is de spanningsdeler vergelijking

Waarbij Vn de spanningsval over de n-de weerstand is, VS de spanningsbron, Rn de weerstand van de n-de weerstand en Req de equivalente serieweerstand.
Voorbeelden van formules voor de spanningsverdeling regel
Laten we nu een paar voorbeelden oplosse
1. Bereken de spanningsval in het onderstaande circuit dat bestaat uit 2 weerstanden die in serie zijn geschakeld
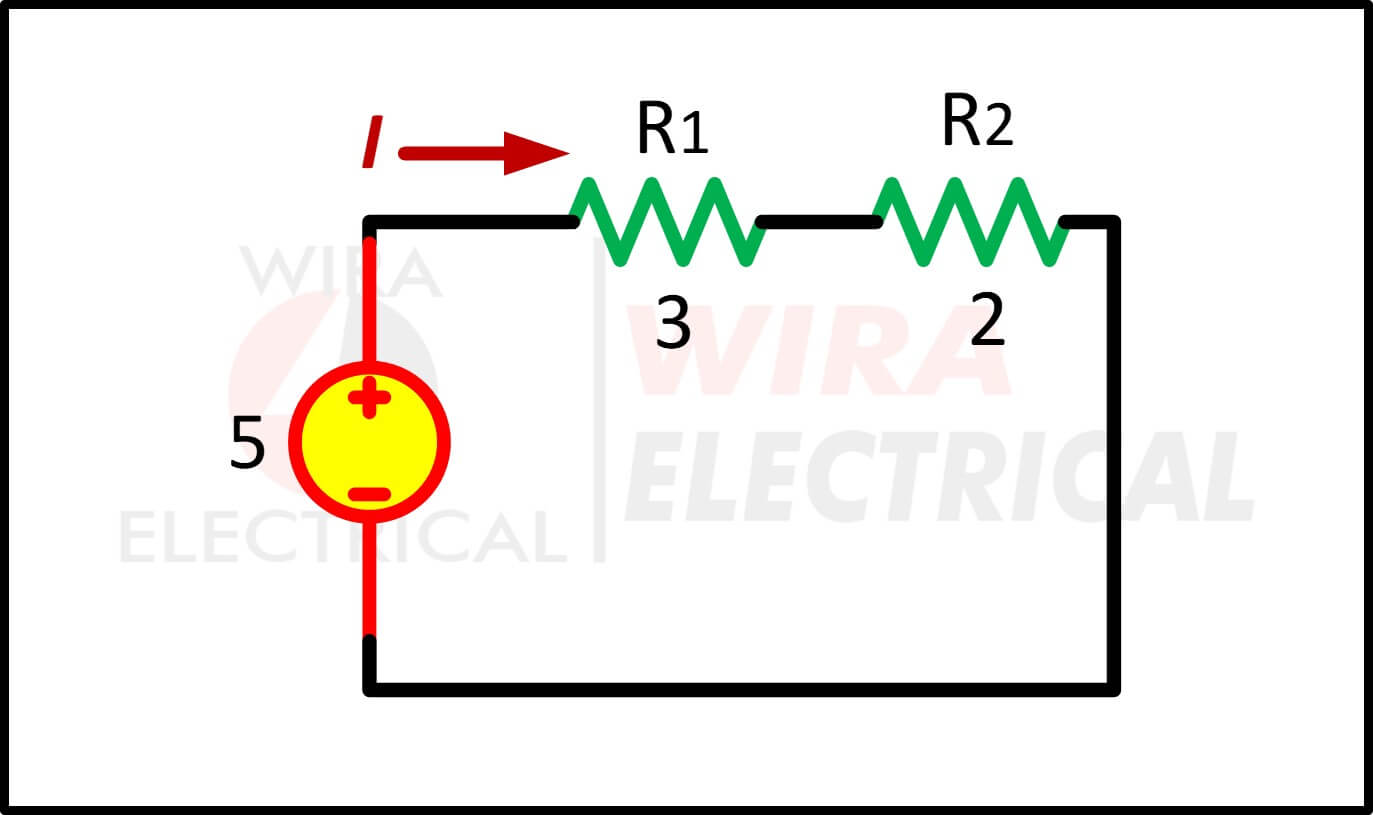
De totale weerstand of equivalente weerstand is

De totale stroom is
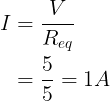
De spanningsval over de R1 is
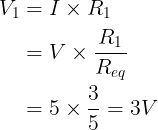
De spanningsval over de R2 is
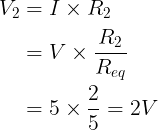
2. Een elektrisch circuit hieronder bestaat uit 3 weerstanden met dezelfde weerstand. Bereken de spanningsval over elke weerstand

De equivalente weerstand is

De totale stroom is
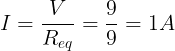
De spanningsval over elke weerstand is
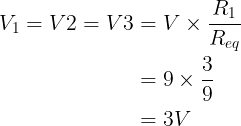
3. Hieronder staat het gemeenschappelijke spanningsdeler circuit met alleen twee weerstanden. We krijgen de gewenste spanning op de VOUT-aansluiting.
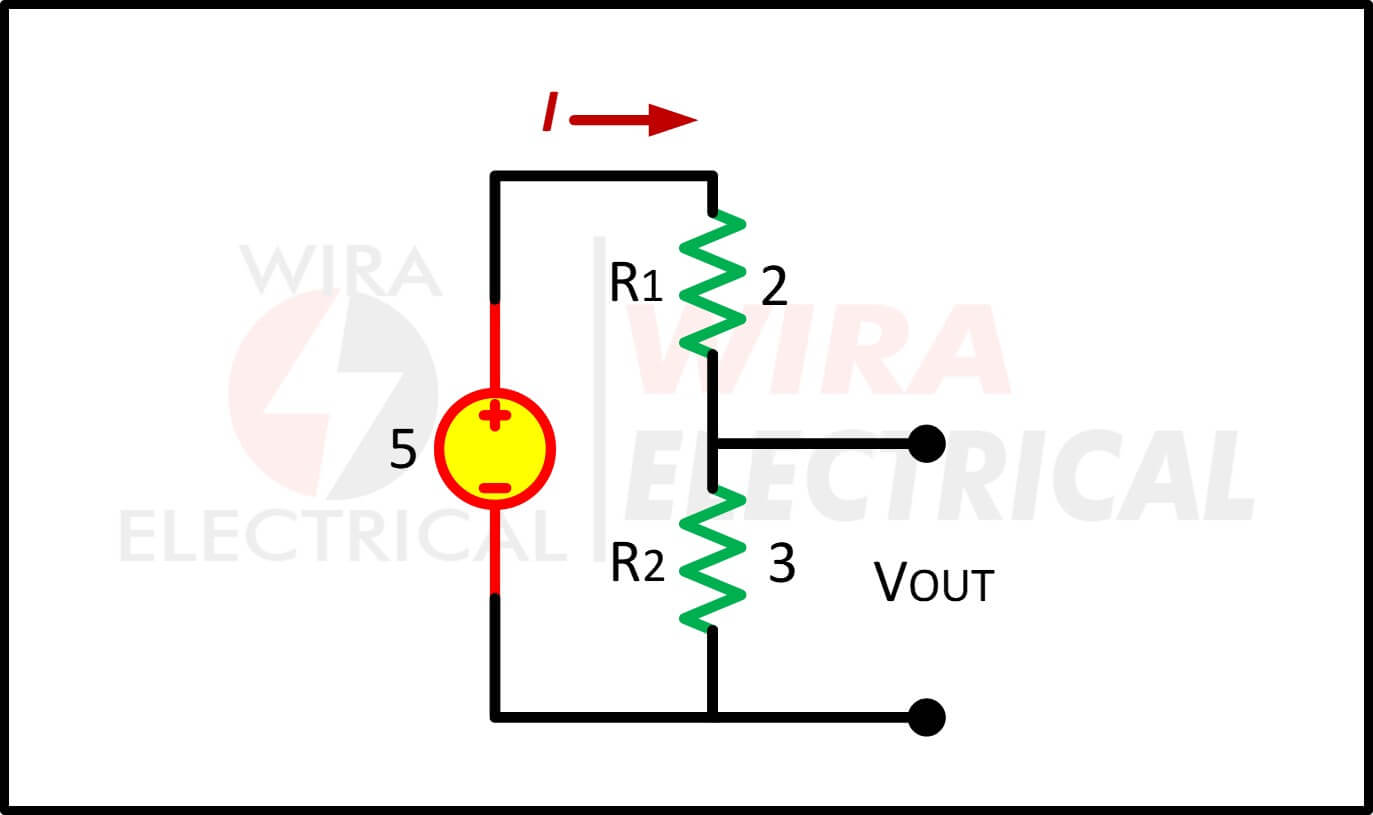
Om direct ter zake te komen: de VOUT zal
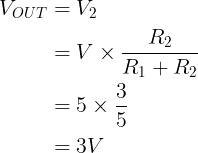
Veelgestelde vragen
Wat is de spanningsverdeling regel?
De spanningsverdeling regel stelt dat de gehele spanning die over een serieschakeling van meerdere weerstanden wordt geleverd, evenredig over de weerstanden wordt verdeeld.
Hoe weet u wanneer u spanningsverdeling moet gebruiken?
Een spanningsverdeling circuit is een circuit om het gewenste spanningsniveau uit de spanningsbron te produceren, maar de stroom is nog steeds hetzelfde. De algemene configuratie van een spanningsverdeling circuit wordt hieronder weergegeven.