Resistor Paralel dan Rangkaian Pembagi Arus – Penjelasan Mudah

Jika persamaan tidak ditampilkan dengan benar, silakan gunakan tampilan desktop

Kalian akan tahu apakah resistor secara paralel atau seri hanya dari koneksi terminalnya. Sambungan resistor paralel adalah terminalnya dihubungkan bersama masing-masing dari resistor ke resistor.

Jika resistor seri hanya memiliki satu jalur untuk arus listrik, resistor paralel memiliki beberapa jalur untuk arus listrik karena mereka memiliki setidaknya satu node. Ini memenuhi hukum Kirchhoff dimana jumlah arus listrik yang masuk ke node sama dengan arus listrik yang keluar dari node itu.

Definisi Rangkaian Paralel

Resistor paralel ini berbeda dengan resistor seri dimana hanya ada satu jalur lurus yang melewati resistor. Pada resistor paralel akan ada banyak jalur dari kepala ke kepala dan ekor ke ekor.

Dari istilah ini, resistor paralel digunakan sebagai pembagi arus, sedangkan resistor seri adalah pembagi tegangan.

Karena arus dibagi menjadi beberapa jalur atau cabang, arus untuk setiap cabang mungkin berbeda satu sama lain. Tapi, drop tegangan untuk setiap resistor akan sama satu sama lain.

Ini menyimpulkan bahwa

Resistor secara paralel mungkin memiliki arus yang berbeda melalui masing-masing tetapi selalu memiliki drop tegangan yang sama di masing-masing resistor.

Jika kita diminta untuk mendefinisikan rangkaian paralel, jawaban terbaik adalah:

Definisi rangkaian paralel adalah rangkaian dimana elemen-elemennya dihubungkan bersama pada node yang sama dan menghasilkan lebih dari satu jalur arus yang dihubungkan pada sumber tegangan yang sama.

Jika kalian masih bingung bagaimana cara membuat rangkaian resistor paralel, kita dapat menemukannya di bawah ini.

Diagram Rangkaian Paralel

Contoh di bawah ini adalah resistor paralel sederhana dalam suatu rangkaian. Kita menggunakan tiga resistor R₁, R₂, dan R₃. Ketiga resistor tersebut dihubungkan bersama antara A dan B.

Dari penjelasan di atas, drop tegangan pada resistor pada sambungan paralel akan bernilai sama satu sama lain dan bernilai sama dengan sumber tegangan.

Karenanya,

$\begin{align*}V_{R1}=V_{R2}=V_{R3}=V_{AB}=12V\end{align*}$

Berbeda dari rangkaian resistif seri di mana resistansi ekivalen adalah jumlah semua resistor, resistor paralel dihitung secara berbeda. Kita menggunakan kebalikan dari resistansi (1/R) untuk setiap resistor yang ditambahkan bersama-sama.

Rumus Resistor Paralel

Seperti yang telah kita amati di atas,

Hambatan ekivalen dari resistor paralel adalah jumlah dari kebalikan dari masing-masing resistor.

Jika resistor yang dihubungkan bersama secara paralel memiliki nilai yang sama maka akan sangat mudah.

Sama seperti yang kita sebutkan di atas, kita dapat melihat contoh di bawah ini:

Jika dua buah resistor yang dirangkai paralel memiliki hambatan yang sama maka hambatan penggantinya, R_eq adalah setengah dari hambatan salah satu resistor. Jadi hambatan pengganti dua buah resistor yang dirangkai paralel jika hambatannya sama adalah R/2. Jika ada tiga resistor yang dirangkai paralel maka hambatan penggantinya adalah R/3, dan seterusnya.

Selain resistor seri, jenis rangkaian ini adalah jenis rangkaian listrik yang paling umum. Untuk menganalisis rangkaian resistor paralel kita dapat menggunakan metode yang sama untuk resistor seri, menggunakan hukum Kirchhoff dan hukum Ohm.

Perhatikan rangkaian di bawah ini,

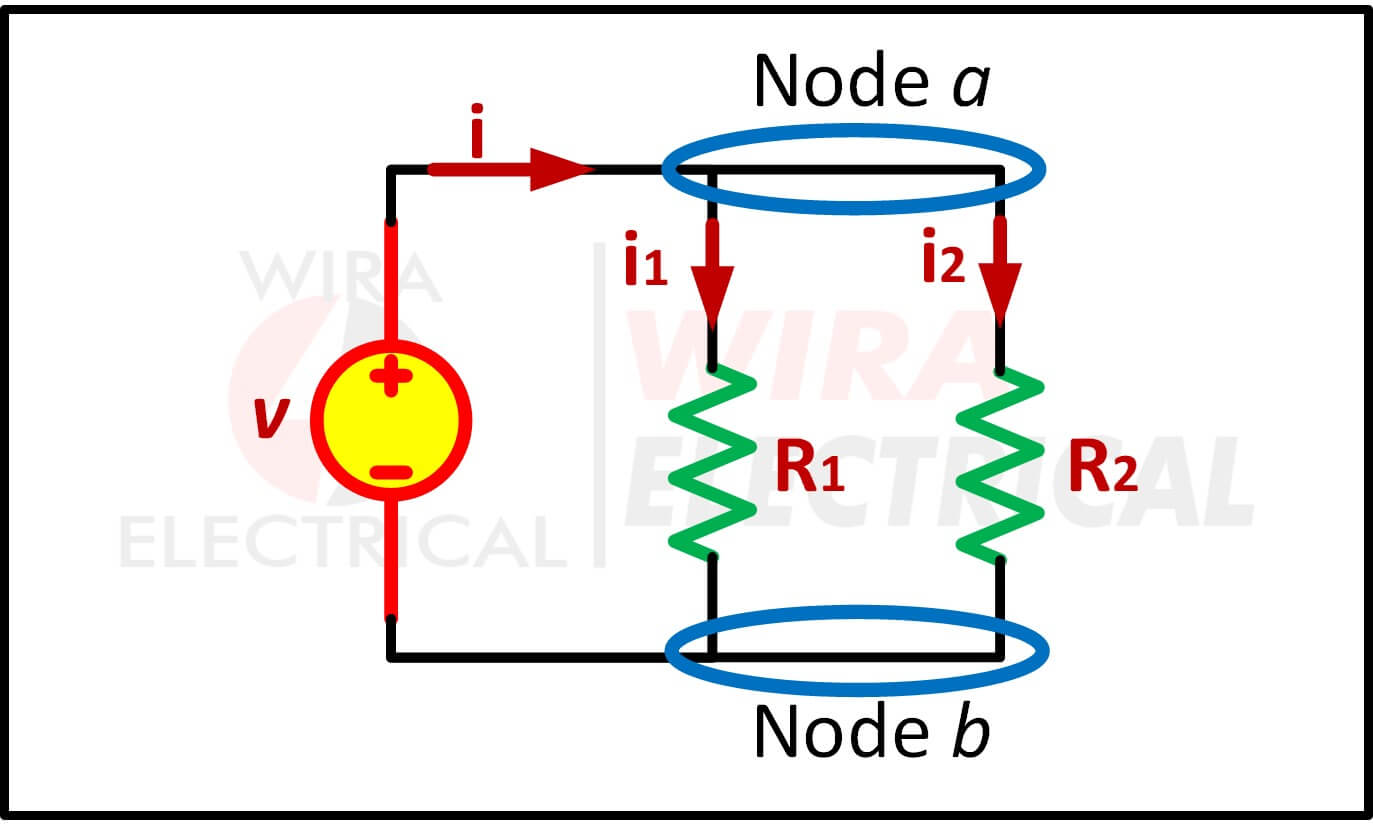
di mana dua resistor dihubungkan secara paralel dan oleh karena itu memiliki tegangan yang sama di antara mereka.

Dari hukum Ohm

$\begin{align*}v=i_{1}R_{1}=i_{2}R_{2}\\i_{1}=\frac{v}{R_{1}},\quad i_{2}=\frac{v}{R_{2}}\end{align*}$

Menerapkan KCL pada node a memberikan arus total i sebesar

$\begin{align*}i=i_{1}+i_{2}\end{align*}$

Mensubstitusikan persamaan untuk tegangan menjadi arus, kita dapatkan

$\begin{align*}i&=\frac{v}{R_{1}}+\frac{v}{R_{2}}\\&=v(\frac{1}{R_{1}}+\frac{1}{R_{2}})\\&=\frac{v}{R_{eq}}\end{align*}$

di mana R_eq adalah resistansi ekivalen dari resistor secara paralel:

$\begin{align*}\frac{1}{R_{eq}}&=\frac{1}{R_{1}}+\frac{1}{R_{2}}\\\frac{1}{R_{eq}}&=\frac{R_{1}+R_{2}}{R_{1}R_{2}}\end{align*}$

atau

$\begin{align*}{R_{eq}}=\frac{R_{1}R_{2}}{R_{1}+R_{2}}\end{align*}$

Jadi,

Hambatan ekivalen dari dua resistor paralel sama dengan produk dari resistansi mereka dibagi dengan jumlah mereka.

Di atas adalah persamaan resistor paralel paling sederhana yang dapat kita gunakan setiap kali kita membutuhkannya.

Perlu dicatat bahwa persamaan R_eq di atas hanya bekerja untuk dua resistor secara paralel.

Kita dapat memperluas resistansi resistor paralel ekivalen ke kasus umum rangkaian dengan N resistor secara paralel. Resistansi ekivalennya adalah

$\begin{align*}\frac{1}{R_{eq}}&=\frac{1}{R_{1}}+\frac{1}{R_{2}}+...+\frac{1}{R_{N}}\end{align*}$

Perhatikan bahwa R_eq selalu lebih kecil dari resistansi resistor terkecil dalam koneksi paralel. Jika R₁ =R₂ = … = R_N = R, maka

$\begin{align*}R_{eq}=\frac{R}{N}\end{align*}$

Misalnya, jika 4 resistor dengan 100Ω dihubungkan secara paralel, resistansi ekivalennya adalah 25Ω.

Ingatlah bahwa,

Resistansi ekivalen resistor paralel selalu lebih kecil dari resistor terkecil yang terhubung ke jaringan itu. Oleh karena itu, resistansi ekivalen, Req, akan berkurang setiap kali kita memiliki resistor paralel tambahan.

Cara Menemukan Arus di Rangkaian Paralel

Karena arus pada rangkaian paralel didasarkan pada hambatannya, sekarang kita akan belajar tentang cara mencari arus pada rangkaian paralel.

Arus I₁, I₂, …, Dalam memasuki jalur paralel resistor tergantung pada resistansi cabang itu. Arus total, I_T adalah jumlah arus di cabang paralel. Jika hambatan antar cabang sama maka arus juga akan terbagi sama rata.

Jika R₁ = R₂ maka I₁ = I₂ = 0.5I_T. Artinya total arus I_T dibagi rata untuk dua cabang. Jika R₁ memiliki hambatan yang berbeda dari R₂ maka kita perlu menghitung I₁ dan I₂ secara berbeda. Bahkan jika tegangan di cabang sama, arus mungkin berbeda menurut hukum Ohm.

Untuk contoh rangkaian paralel mari kita lihat rangkaian di bawah ini dan coba cari semua arus secara paralel,

Karena R₁ dan R₂ memiliki nilai yang berbeda, maka arus I₁ dan I₂ dijamin memiliki nilai yang berbeda. Ingat salah satu hukum Kirchhoff?

Hukum Kirchhoff arus menyatakan:

Arus total yang keluar dari suatu node sama dengan arus yang masuk ke node yang sama.

Karenanya,

Arus total dalam rangkaian dapat dinyatakan sebagai:

$\begin{align*}I_{T}=I_{R1}+I_{R2}\end{align*}$

Setelah itu, kita akan menggunakan hukum Ohm untuk menghitung arus yang masuk ke setiap cabang melalui resistor. I₁ adalah arus yang masuk ke R₁ sedangkan I₂ adalah arus yang masuk ke R₂. Sumber tegangan V_s memiliki 12V dan kita mendapatkan:

$\begin{align*}I_{1}&=\frac{V_{s}}{R_{1}}=\frac{12}{3}=4A\\I_{2}&=\frac{V_{s}}{R_{2}}=\frac{12}{6}=2A\end{align*}$

Dan kita mendapatkan arus total,

$\begin{align*}I_{T}=I_{R1}+I_{R2}=4+2=6A\end{align*}$

Untuk memperjelas hal ini, kita menggunakan hukum Ohm untuk menghitung I_T dari V_s dan R_eq.

Resistansi ekivalen R_eq adalah

$\begin{align*}R_{eq}=\frac{R_{1}R_{2}}{R_{1}+R_{2}}=\frac{3\times6}{3+6}=2\Omega\end{align*}$

Maka arus total I_T adalah

$\begin{align*}I_{T}=\frac{V_{s}}{R_{eq}}=\frac{12}{2}=6A\end{align*}$

Oleh karena itu, ini memperjelas perhitungan kita.

Kita menyimpulkan bahwa

$\begin{align*}I_{total}=I_{1}+I_{2}+...+I_{n}\end{align*}$

Persamaan Pembagi Arus

Setelah belajar tentang resistor paralel, kita akan belajar tentang aturan pembagi arus.

Jika kalian telah belajar tentang pembagi tegangan, pembagi arus agak mirip dan agak tidak mirip.

Persamaan pembagi tegangan dapat menyelesaikan perhitungan drop tegangan terlepas dari jumlah resistor. Tapi untuk pembagi arus, itu sangat berbeda.

Rumus pembagi arus dapat digunakan untuk dua resistor. Kita akan menemukan alasan mengapa aturan pembagi arus untuk 3 resistor secara paralel perlu kita selesaikan dengan pendekatan yang berbeda.

Menggabungkan

$\begin{align*}v=i_{1}R_{1}=i_{2}R_{2}\\i_{1}=\frac{v}{R_{1}},\quad i_{2}=\frac{v}{R_{2}}\end{align*}$

dan

$\begin{align*}v=iR_{eq}=i\frac{R_{1}R_{2}}{R_{1}+R_{2}}\end{align*}$

Akan memberi kita persamaan pembagi arus

$\begin{align*}i_{1}&=\frac{R_{2}}{R_{1}+R_{2}}i\\i_{2}&=\frac{R_{1}}{R_{1}+R_{2}}i\end{align*}$

yang menunjukkan arus total i dibagi oleh resistor dalam proporsi terbalik dengan resistansi mereka.

Ini dikenal sebagai prinsip pembagian arus, dan rangkaian di atas dikenal sebagai pembagi arus.

Perhatikan bahwa arus yang lebih besar mengalir melalui hambatan yang lebih kecil.

Misalkan salah satu resistor dalam rangkaian adalah nol, katakanlah R₂ = 0; jadi R₂ adalah hubung singkat, seperti dapat dilihat pada rangkaian di bawah ini.

Dari persamaan pembagi arus, R₂ = 0 menyiratkan bahwa i₁ = 0, i₂ = i. Ini berarti bahwa seluruh arus i melewati R₁ dan mengalir melalui hubung singkat R₂ = 0, jalur dengan hambatan paling kecil.

Ketika sebuah rangkaian dihubung pendek seperti dapat dilihat di atas, perhatikan bahwa:

Resistansi ekivalen R_eq = 0

Seluruh arus mengalir melalui hubung singkat.

Untuk contoh ekstrim lain di mana R₂ = ∞, yaitu R₂ adalah rangkaian terbuka seperti yang dapat dilihat pada rangkaian di bawah ini.

Arus masih mengalir melalui jalur dengan hambatan paling kecil, R₁.

Persamaan pembagi arus menjadi

$\begin{align*}i_{1}&=\frac{G_{1}}{G_{1}+G_{2}}i\\i_{2}&=\frac{G_{2}}{G_{1}+G_{2}}i\end{align*}$

Secara umum, jika pembagi arus memiliki N konduktor yang paralel dengan arus sumber i, konduktor ke-N akan memiliki arus

$\begin{align*}i_{n}=\frac{G_{n}}{G_{1}+G_{2}+...+G_{N}}i\end{align*}$

Sangat mudah untuk menggabungkan resistor secara seri dan paralel menjadi resistansi setara tunggal R_eq.

Resistansi ekivalen tersebut harus memiliki nilai arus dan tegangan yang sama dengan jaringan asli di terminal.

Setelah mencapai titik ini, kita dapat menyimpulkan bahwa,

Aturan pembagi arus untuk 3 resistor secara paralel mengharuskan kita untuk menemukan resistansi yang setara, drop tegangan paralel, dan akhirnya arus yang sesuai.

Contoh Resistor Paralel

Mari kita tinjau contoh di bawah ini untuk pemahaman yang lebih baik. Kita akan mencoba lebih dari 3 resistor secara paralel sebagai contoh.

Temukan R_eq untuk rangkaian di bawah ini.

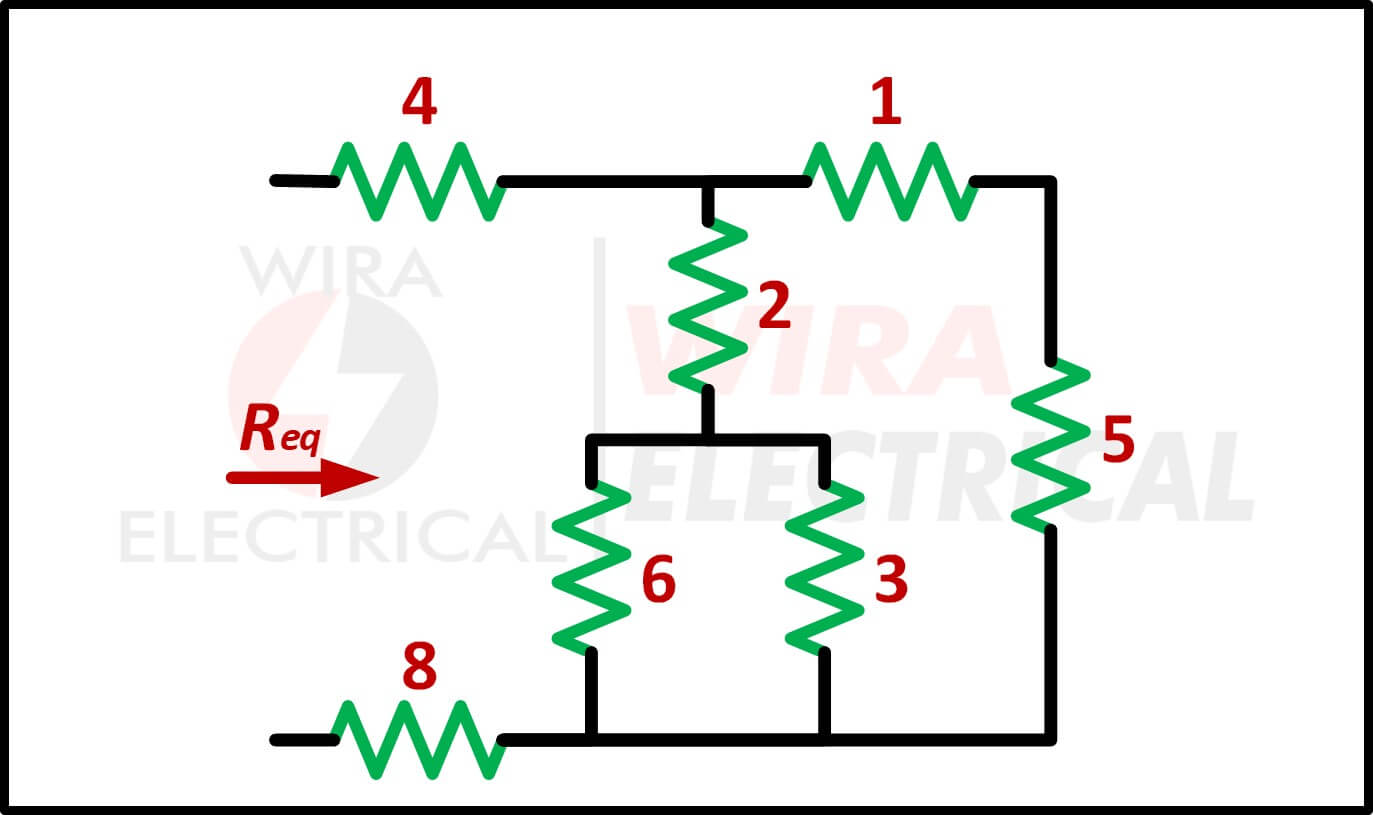
6Ω dan 3Ω secara paralel

$\begin{align*}6\Omega\parallel 3\Omega=\frac{6\times 3}{6+3}=2\Omega\end{align*}$

1Ω dan 5Ω secara seri

$\begin{align*}1\Omega +5\Omega=6\Omega\end{align*}$

2Ω dan 2Ω secara seri

6Ω dan 4Ω secara paralel

$\begin{align*}4\Omega\parallel 6\Omega=\frac{4\times 6}{4+6}=2.4\Omega\end{align*}$

Tiga resistor secara seri

Hambatan pengganti untuk resistor paralel adalah

$\begin{align*}R_{eq}=4\Omega+2.4\Omega+8\Omega=14.4\Omega\end{align*}$

Pertanyaan yang Sering Diajukan

Mengapa resistor yang dirangkai paralel disebut pembagi arus?

Tegangan pada resistor paralel memiliki nilai yang sama tetapi arus yang berbeda untuk setiap cabang (jika hambatan setiap cabang memiliki nilai yang berbeda). Ini juga memenuhi Hukum Arus Kirchhoff.

Bagaimana cara menghitung rangkaian paralel arus?

Arus total dalam rangkaian paralel adalah jumlah dari semua arus pada masing-masing cabang. Dengan kata lain, arus total IT = I1 + I2 + I3. Ini memenuhi Hukum Arus Kirchhoff.

Apa rumus hambatan paralel?

Resistansi ekivalen untuk resistor paralel dapat diperoleh dari rumus: 1/Req = 1/R1 + 1/R2 + 1/R3 + … + 1/RN. Perlu diingat bahwa resistansi ekivalen untuk resistor paralel selalu lebih kecil dari resistansi individu terkecil.

Mengapa resistor secara paralel memiliki tegangan yang sama?

Resistor yang terhubung secara paralel ke node yang sama akan memiliki drop tegangan yang sama. Jika ada resistor yang terhubung secara paralel tetapi ke node yang berbeda, resistor tersebut mungkin memiliki drop tegangan yang berbeda dan tidak dianggap terhubung secara paralel dengan resistor paralel lainnya meskipun terhubung secara paralel.

Apakah resistor secara paralel memiliki tegangan yang sama?

Drop tegangan pada setiap individu resistor paralel akan sama satu sama lain. Tetapi arus yang mengalir melaluinya mungkin berbeda tergantung pada resistor terkait menggunakan Hukum Ohm.

Apakah tegangan dibagi dalam rangkaian paralel?

Tegangan melintasi komponen paralel yang terhubung ke node yang sama adalah sama. Arus total dalam rangkaian paralel adalah jumlah arus setiap cabang yang terhubung ke node itu.

Apakah arus terbagi merata pada rangkaian paralel?

Arus tidak selalu terbagi rata dalam rangkaian paralel. Arus yang mengalir di setiap cabang tergantung pada resistansi atau impedansinya, yang diperoleh dari hukum Ohm.

Apakah resistor paralel memiliki arus yang sama?

Drop tegangan pada setiap individu resistor paralel akan sama satu sama lain. Tetapi arus yang mengalir melaluinya mungkin berbeda tergantung pada resistor terkait menggunakan Hukum Ohm.

Bagaimana distribusi arus pada rangkaian paralel?

Dalam rangkaian paralel, arus total terbagi menjadi beberapa cabang yang terhubung ke node yang sama dan bergabung bersama ke node setelah melewati elemen. Arus total sebelum dipisah akan sama dengan arus total setelah digabungkan.

Bagaimana cara mengetahui apakah dua resistor paralel?

Sambungan resistor paralel adalah terminalnya dihubungkan bersama masing-masing dari resistor ke resistor.

Bagaimana cara mengetahui resistor paralel atau seri?

Jika arus tidak dibagi menjadi beberapa cabang maka itu adalah rangkaian seri karena hanya memiliki jalur arus tunggal. Rangkaian paralel memiliki beberapa jalur arus.

Cara membuat diagram rangkaian paralel

Untuk membuat rangkaian paralel kita hanya perlu menghubungkan head-to-head dan tail-to-tail untuk setiap elemen yang ingin kita hubungkan secara paralel.

Bagaimana menemukan arus melintasi resistor

Untuk menemukan arus melintasi resistor kita dapat menggunakan Hukum Ohm di mana I = V/R.