Bentuk gelombang sinusoidal merupakan bentuk gelombang yang berosilasi secara periodik atau mempunyai frekuensi dan memenuhi perhitungan sinus. Bentuk gelombang ini berbentuk S, naik turun secara periodik dengan amplitudo positif dan negatif.
Tentunya tidak hanya fungsi sinus saja, kita juga dapat membuat bentuk gelombang sinusoidal dengan fungsi kosinus. Bentuknya akan sama tetapi titik awalnya berbeda.
![]()
Jika kamu sudah mempelajari fungsi sinus dan cosinus, kamu akan menyadari bahwa fungsi cosinus bergeser 90o ke fungsi sinus.
Ambil contoh waktu x = 0 (sumbu X).
![]()
Pada jangka waktu yang tepat, sinus akan dimulai dari 0 sedangkan kosinus akan dimulai dari 1. Semoga ini bisa membantu sebelum melangkah lebih jauh.
Apa itu Sinyal Listrik?
Arus bolak-balik sinusoidal dan tegangan sinusoidal adalah jenis sinyal listrik. Sinyal ini mempunyai besaran listrik, baik berupa tegangan maupun arus. Kita dapat menggunakan ini untuk mengumpulkan informasi dari satu titik ke titik lain melalui media seperti elektromagnetik, kawat, dll.
Namun memanfaatkan sinyal ini tidaklah sesederhana kedengarannya, kita perlu menganalisis bentuk gelombang, amplitudo, jarak, medium, dan perilaku sinyal yang ditransmisikan. Grafik yang digunakan untuk menganalisis bentuk gelombang ini juga dikenal sebagai representasi bentuk gelombang sinusoidal.
Perlu diingat, sinyal yang digunakan untuk menyampaikan suatu informasi terdiri dari sinyal pesan dan sinyal pembawa. Seperti bunyinya, sinyal pesan adalah sinyal yang berisi informasi, sedangkan sinyal pembawa adalah energi yang diperlukan untuk aliran sinyal.
Representasi Bentuk Gelombang Sinusoidal pada Rangkaian AC
Sekarang kita akan membahas tentang bentuk gelombang sinusoidal. Sinyal periodik pada rangkaian AC dengan fungsi sinus atau fungsi kosinus dalam trigonometri disebut representasi bentuk gelombang sinusoidal pada rangkaian AC. Sinyal sinusoidal ini juga dikenal sebagai sinusoidal.
Seperti yang telah disebutkan di atas, bentuk gelombang ini berbentuk huruf S dalam jangka waktu tertentu. Jika kita amati lebih dalam, bentuk S ini terdiri dari sepasang busur atau setengah lingkaran dengan amplitudo positif dan negatif.
Untuk pemahaman yang lebih baik, saat menggambar bentuk gelombang sinusoidal kita akan menggunakan grafik dua dimensi yang terdiri dari sumbu X dan sumbu Y.
Bentuk gelombang sinusoidal mempunyai amplitudo yang menunjukkan nilai maksimum atau nilai puncaknya.
Sumbu X akan menjadi sumbu waktu dan sumbu Y akan menjadi sumbu amplitudo.
Seperti yang sudah kita baca di atas, kita bisa menggunakan fungsi cosinus atau sinus untuk membentuk sinusoida hanya dengan titik awal yang berbeda.
![]()
⍵ adalah frekuensi sudut dalam rad/s (radian per detik)
⍵t adalah argumen sinusoidal
Fungsi sinus akan menghasilkan sinyal gelombang sinus sedangkan fungsi cosinus akan menghasilkan sinyal gelombang kosinus.
Jika t = 0 pada sumbu X, maka
Sinyal gelombang sinus akan memiliki titik awal pada 0 pada sumbu Y. Nilai amplitudonya akan naik menjadi 1 ketika ⍵t = 90 kemudian turun ke nol lagi ketika ⍵t = 180 kemudian turun lagi ke -1 ketika ⍵t = 270 dan naik ke nol ketika ⍵t = 360.

Sinyal gelombang kosinus akan memiliki titik awal pada 1 di sumbu Y. Nilai amplitudonya akan turun menjadi 0 ketika ⍵t = 90 lalu turun menjadi -1 ketika ⍵t = 180 lalu naik menjadi 0 ketika ⍵t = 270 dan naik lagi menjadi 1 pada ⍵t = 360.

Bentuk gelombang sinusoidal memiliki nilai kontinu tergantung pada ⍵t. Ini memiliki nilai sesaat pada stempel waktu tertentu. Karena bergantung pada waktu, maka dapat disimpulkan bahwa bentuk gelombang sinusoidal merupakan fungsi waktu dan ditulis sebagai fungsi waktu f(t).
Apa yang dimaksud dengan Radian pada AC Sinusoidal
Radian atau disingkat rad, secara matematis, adalah satuan sudut dalam Sistem Satuan Internasional dan merupakan satuan standar ukuran sudut yang digunakan di banyak bidang matematika. Didefinisikan sedemikian rupa sehingga satu radian adalah sudut yang dibentuk di pusat lingkaran oleh busur yang panjangnya sama dengan jari-jarinya.
1 rad jika diubah menjadi derajat maka akan menjadi
180 / π = 57.296o
Atau karena lingkaran penuh 360o sama dengan 2π maka
![]()
Atau kita bisa menggunakan persamaan di bawah ini

Dengan beberapa contoh:
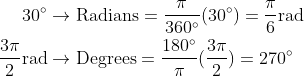
Bentuk Gelombang Sinusoidal AC
Perhatikan contoh Bentuk Gelombang Sinusoidal Arus Bolak-balik di bawah ini.

Dari bentuk gelombang sinusoidal di atas, kita tuliskan fungsi sinusoidal gelombang sinus ac
![]()
Di mana:
v(t) = fungsi waktu
Vm = amplitudo sinusoidal
⍵ = frekuensi sudut dalam rad/s
⍵t = argumen sinusoida
T = periode waktu
π = perbandingan keliling lingkaran dengan diameternya
Mengapa kita menggunakan π?
Karena variabel ini mewakili lingkaran penuh yang dipotong menjadi dua membentuk bentuk gelombang sinusoidal.
Dari bentuk gelombang di atas kita dapat melihat siklus berulang suatu sinusoidal setiap T detik, sehingga T inilah yang kita sebut periode sinusoida.
Membandingkan kedua bentuk gelombang tersebut kita dapat menyimpulkan bahwa ⍵T = 2π. Dengan demikian
![]()
Kita dapat melihat bahwa v(t) mempunyai nilai berulang setiap T detik, dengan t digantikan oleh t + T

Dengan demikian
![]()
Fungsi periodik adalah fungsi yang memenuhi f(t) = f(t + nT), untuk semua t dan untuk semua bilangan bulat n.
Tolong jangan berpikir t dan T itu sama. T menunjukkan waktu sedangkan T menunjukkan periode atau waktu yang diperlukan untuk menyelesaikan satu siklus atau jumlah detik per siklus.
Nilai kebalikan atau timbal balik periode (T) adalah frekuensi (f) yang diukur dalam Hertz atau Hz. Frekuensi menunjukkan jumlah siklus per detik.
![]()
Semakin tinggi frekuensinya berarti semakin banyak siklus yang terjadi dalam satu detik atau semakin sedikit waktu yang diperlukan untuk menyelesaikan satu siklus.
Dengan demikian,
![]()
Persamaan gelombang sinusoidal merupakan perkalian amplitudo tegangan dengan fungsi sinus dari jumlah argumen sinusoidal dengan fasa.
![]()
Seperti disebutkan di atas, ⍵t adalah argumen sinusoidal dan ∅ adalah fasenya. Keduanya bisa dalam satuan radian atau derajat.
Untuk persamaan gelombang sinusoidal yang lebih lengkap, kita dapat menggunakan salah satu persamaan di bawah ini.
![]()
Persamaan bentuk gelombang sinusoidal dengan fasa akan menunjukkan apakah bentuk gelombang tersebut lag atau lead berdasarkan radian atau derajat. Perhatikan bentuk gelombang sinusoidal di bawah ini.
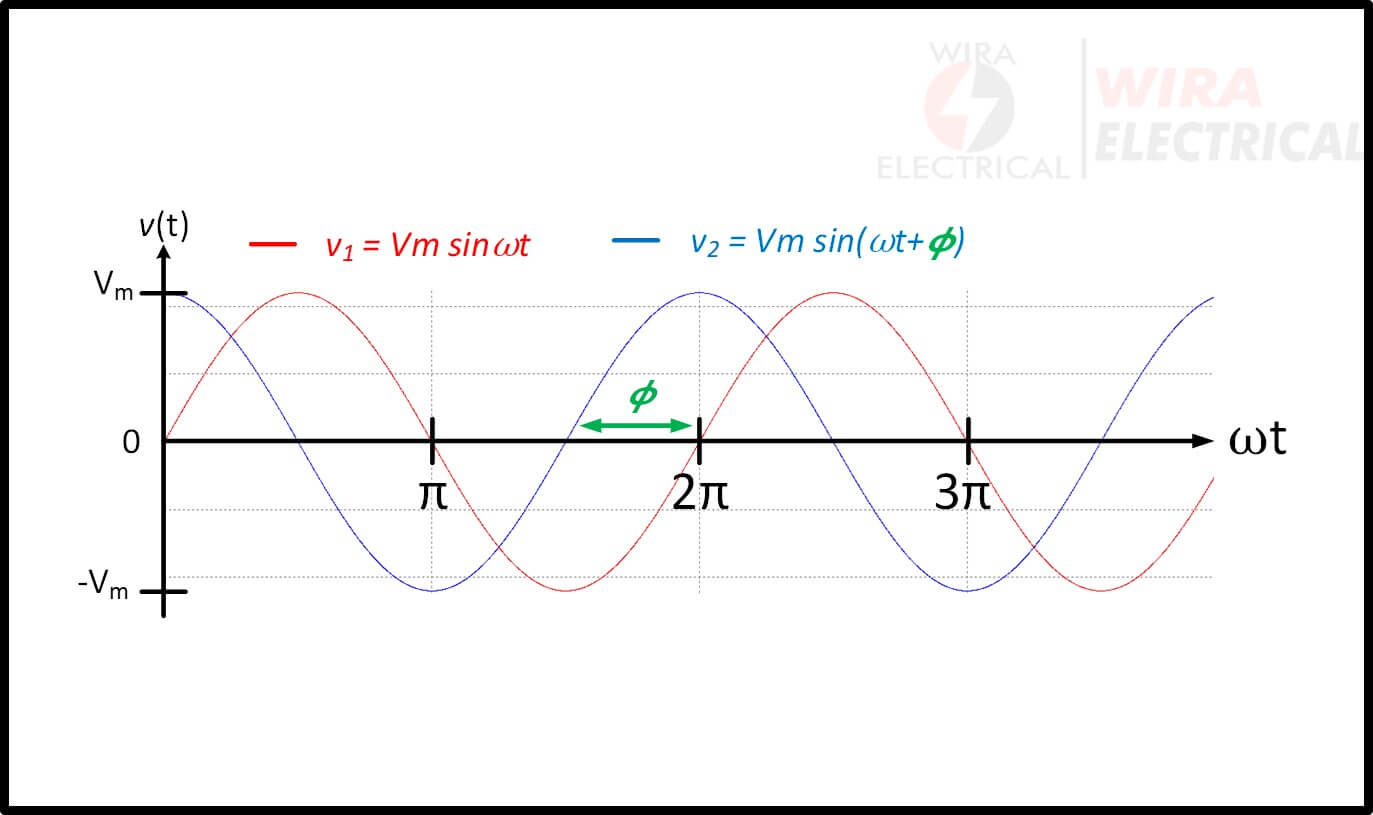
Dengan persamaan di atas, kita dapat melihat bahwa:
- v2 memimpin v1 dengan ∅ (dimulai sebelum ⍵t = 0)
- v1 tertinggal dari v2 sebesar ∅ (dimulai pada ⍵t = 0)
Contoh Persamaan Gelombang Sinus AC
Kita akan mempelajari cara menggunakan persamaan gelombang sinus AC dengan amplitudo, fase, periode, dan frekuensi yang diketahui dalam fungsi di bawah ini.
![]()
Dari fungsi sinus di atas kita peroleh beberapa variabel:
v(t) = sinusoidal ac
Amplitudo = 12
Fase (∅) = 10o
Frekuensi sudut (⍵) = 50 rad/s
Dengan diketahuinya frekuensi sudut, kita dapat menghitung periode waktu dan frekuensinya

Mengapa Bentuk Gelombang Sinusoidal Digunakan untuk AC
Sekarang tidak sulit untuk menjelaskan mengapa bentuk gelombang sinusoidal penting dalam aspek kelistrikan dan elektronik dan digunakan untuk rangkaian AC. Bentuk gelombang ini adalah representasi alami dari arus bolak-balik. Bentuk gelombang ini berosilasi tanpa henti ketika disuplai ke rangkaian dengan frekuensi, amplitudo, dan fase tertentu.
Bentuk gelombang osilasi ini memiliki fungsi matematika tersendiri yang dapat digunakan untuk penjumlahan, pengurangan, perkalian, dan pembagian.
Jadi mengapa bentuk gelombang sinusoidal?
Hal ini dapat kita lihat pada generator AC saat beroperasi. Gerakan melingkar ke generator mewakili bentuk gelombang sinusoidal jika polaritas positif dan polaritas negatif digabungkan untuk membentuk bentuk lingkaran sempurna.
Katakanlah kita memutar poros generator AC 180o maka akan menghasilkan gelombang sinus periode positif dan jika kita terus memutar poros dari 180o ke 360o maka akan menghasilkan gelombang sinus periode negatif.
Proses ini diulangi dan menghasilkan bentuk gelombang sinusoidal yang berosilasi.