Apa itu Diagram Fasor dan Bilangan Kompleks

Fasor dapat digunakan untuk menggambarkan gelombang sinusoidal dengan mudah, dimana metode yang praktis daripada menggunakan fungsi sinus atau cosinus.

Fasor adalah bilangan kompleks yang mewakili amplituda dan fase sebuah sinusoidal.

Fasor memberikan metode sederhana untuk menganalisa rangkaian linear yang memperoleh energi dari sumber sinusoidal. Usaha untuk menyelesaikan rangkaian ac menggunakan metode ini diperkenalkan pertama kali oleh Charles Steinmetz pada tahun 1893. Sebelum kita mempelajari fasor, kita harus menguasai bilangan kompleks terlebih dahulu.

Diagram Fasor dan Bilangan Kompleks

Bilangan kompleks z dapat dinyatakan dalam bentuk rectangular (persegi panjang) seperti

(1a)

dimana j = (√-1); x adalah nilai nyata (real) dari z; sedangkan y adalah nilai imajiner (imaginary) dari z.

Kali ini, x dan y tidak merujuk pada kordinat atau lokasi seperti pada vektor dua dimensi, tetapi merujuk pada nilai nyata dan imajiner dari z pada bidang kompleks. Meskipun, akan ada penggunaan bilangan komples dengan metode analisa vektor dua dimensi.
Bilangan kompleks z juga dapat digambarkan alam bentuk polar dan eksponensial seperti

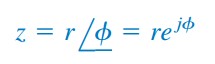(1b)

dimana r adalah nilai dari z, dan ∅ adalah fase dari z. Kita dapat menyimpulkan bahwa z dapat digambarkan dalam tiga bentuk :

(2)

Hubungan antara bentuk rectangular dan bentuk polar dapat dilihat pada Gambar.(1), dimana sumbu x mewakili nilai nyata dan sumbu y mewakili nilai imajiner.

Gambar 1. Gambaran nilai kompleks z

Dengan nilai x dan y, kita dapat menghitung r dan ∅ dengan

(3a)

Sebaliknya, jika kita memiliki r dan ∅, kita dapat menghitung x dan y dengan

(3b)

Jadi, z dapat ditulis ulang menjadi

(4)

Pengurangan dan pertambahan dari bilangan kompleks dapat dengan mudah dilakukan pada bentuk rectangular; perkalian dan pembagian dapat dengan mudah dilakukan pada bentuk polar. Dengan bilangan kompleks :

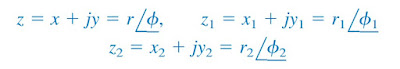(5)

Kita dapat menggunakan operasi berikut :
Pertambahan

(6a)

Pengurangan

(6b)

Perkalian

(6c)

Pembagian

(6d)

Kebalikan

(6e)

Akar kuadrat

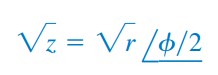(6f)

Konjugasi kompleks

(6g)

Perhatikan Persamaan.(6e)

(6h)

Semua persamaan ini dibutuhkan sebagai operasi dasar bilangan kompleks. Teori dasar yang mewakili fasor berdasarkan identitas Euler. Secara umum,

(7)

yang menunjukkan bahwa kita dapat menganggap cos∅ dan sin∅ sebagai nilai nyata dan imajiner dari e^j∅, kita dapat menulis

(8a)

(8b)

dimana Re dan Im adalah nilai nyata dari dan nilai imajiner dari. Diberikan sebuah contoh sinusoidal v(t) = V_m cos(ωt + ∅), kita gunakan Persamaan.(8a) untuk menyatakan v(t) sebagai

(9)

atau

(10)

Sehingga

(11)

dimana

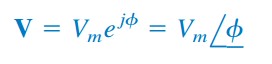(12)

Sehingga, V adalah perwakilan fasor dari sinusoidal v(t), seperti yang telah kita pelajari sebelumnya. Sesuai nama, fasor adalah sebuah perwakilan bilangan kompleks untuk nilai dan fase sebuah gelombang sinusoidal. Kita dapat menggunakan Persamaan.(8a) atau (8b) untuk membuat fasor, tetapi standar konversi berada di Persamaan.(8a)

Coba lihat Persamaan.(11) dan (12) sekali lagi untuk melihat sinor Ve^jωt = V_me^{j(ωt + ø)} pada bidang kompleks. Seiring bertambahnya waktu, sinor bergerak melingkar pada sebuah lingkaran dengan radius V_m dengan kecepatan anguler ω dengan arah berlawanan jarum jam, seperti yang digambarkan Gambar.(2a). Dapat kita asumsikan v(t) sebagai proyeksi dari sinor Ve^jωt pada sumbu real, seperti yang digambarkan Gambar.(2b).

Nilai dari sinor pada t = 0 adalah fasor V dari sinusoidal v(t). Sinor dapat diasumsikan sebagai fasor yang melingkar. Sehingga, kapanpun sinusoidal terbentuk sebagai fasor, istilah e^jωt akan ada secara implisit. Kita harus perhatikan frekuensi ω pada fasor, atau kesalahan akan terjadi.

Gambar 2. Perwakilan Vejωt : (a) sinor berputar berlawanan arah jarum jam, (b) proyeksinya pada sumbu real, sebagai fungsi waktu

Persamaan.(11) merujuk pada cara untuk memperoleh sinusoidal dengan fasor V, kalikan fasor dengan faktor waktu e^jωt dan ambil nilai nyatanya. Sebuah fasor dapat dinyatakan dalam bentuk rectangular, polar, dan eksponensial. Fasor bekerja sebagai vektor dan ditulis dengan cetak tebal (bold) karena merupakan nilai dan fase (arah). Sebagai contoh, V = V_m∠∅ dan I = I_m∠∅ digambar dalam grafik di Gambar.(3). Nama dari gambar grafik ini adalah diagram fasor.

Persamaan.(9) sampai (11) menunjukkan bahwa kita sebaiknya menyatakan sinusoidal dalam bentuk cosinus terlebih dahulu sehingga sinusoidal dapat dibentuk sebagai angka real dari bilangan kompleks untuk memperoleh fasor yang berkaitan. Setelah itu, kita ambil e^jωt dan apapun yang tersisa adalah fasor yang berkaitan dengan sinusoidal. Metode transformasi ini ditulis sebagai berikut,

(13)

Gambar 3. Diagram fasor dari V = Vm∠∅ dan I = Im∠∅

Asumsikan kita memiliki sinsuoidal v(t) = V_m cos(ωt + ∅), kita peroleh fasor V = V_m∠∅. Persamaan.(13) juga muncul di Tabel.(1), dimana fungsi sinus dianggap sebagai tambahan untuk fungsi cosinus. Dari Persamaan.(13), kita anggap untuk memperoleh perwakilan fasor dari sebuah sinusoidal, kita dapat menyatakan dalam bentuk cosinus dan ambil nilainya sebagai fasor dan argument sebagai ωt ditambah fase dari fasor.

Tabel 1

Amati bahwa di Persamaan.(13), faktor frekuensi fasor (atau waktu) e^jωt dihilangkan, dan frekuensi tidak ditunjukkan secara eksplisit di perwakilan domain fasor karena ω adalah konstan. Namun, respon bergantung pada ω. Untuk alasan ini, domain fasor juga dikenal dengan domain frekuensi.

(14)

Dari persamaan di atas, nilai derivatif v(t) ditransformasikan dalam domain fasor sebagai jω. Diferensial sebuah sinusoidal ekuivalen dengan mengalikannya dengan fasor yang berkaitan oleh jω.

(15)

Begitu juga, integral dari v(t) ditransformasikan ke domain fasor sebagai V/jω. Mengintegralkan sebuah sinusoidal ekuivalen dengan membagi fasor yang berkaitan oleh jω.

(16)

Persamaan.(15) dan (16) berguna untuk menentukan solusi stabil (steady-state), dimana tidak perlu untuk mengetahui nilai awal dari variabel yang terlibat. Aplikasi lain yang penting dari fasor adalah menemukan pertambahan dua sinusoidal dengan frekuensi yang sama.

Perbedaan antara v(t) dan V perlu didefinisikan :

• v(t) adalah perwakilan domain waktu atau nilai sesaat, sedangkan V adalah perwakilan domain fasor atau frekuensi
• v(t) bergantung pada waktu sedangkan V tidak
• v(t) selalu bernilai real tanpa istilah kompleks, tetapi V secara umum kompleks

Dari pernyataan di atas, kita simpulkan bahwa analisa fasor hanya berlaku ketika frekuensi konstan; metode ini berlaku dalam memanipulasi dua atau lebih sinyal sinusoidal jika berada di frekuensi yang sama.

Baca juga : analisis supernode

Contoh Soal Diagram Fasor dan Bilangan Kompleks

Untuk penjelasan yang lebih baik mengenai fasor, mari kita simak contoh di bawah :
1. Evaluasi bilangan kompleks di bawah :

Solusi :
(a) Dengan transformasi polar ke rectangular,

Menambahkan keduanya menghasilkan

Melalui akar kuadrat,

(b) Dengan transformasi polar-rectangular, penambahan, perkalian, pembagian

2. Transformasikan sinusoidal berikut ke fasor :

Solusi :
(a) i = 6 cos(50t – 40^o) memiliki

(b) Karena -sin A = cos(A + 90^o),

Bentuk fasor dari v adalah

3. Temukan sinusoidal yang mewakili fasor berikut

Solusi :
(a) Kita tulis ulang

Transformasikan ini ke domain waktu menjadi

(b) Karena  j = 1∠90^o,

Konversikan ini ke domain waktu menjadi

4. Diberikan i₁(t) = 4 cos(ωt + 30^o) A dan i₂(t) = 5 sin(ωt – 20^o) A, temukan jumlahnya
Solusi :
Sekarang kita menemukan aplikasi penting dari : tentukan penjumlahan dari frekuensi yang sama. Arus i₁(t) adalah bentuk standar. Fasornya adalah

Kita harus menyatakan i₂(t) dalam bentuk cosinus. Aturan untuk mengubah sinus ke cosinus adalah pengurangan 90^o. Sehingga,

dan

Jika kita gunakan i = i₁ + i₂, jadi

Transformasikan hasilnya ke domain waktu menjadi